venn
jerey:
diagramy venna
robie zadania z relacji zdarzen A i B, ucze sie diagramu venna
mam kilka pytan .
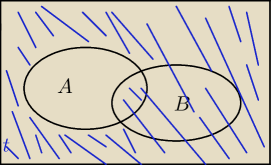
te niebieskie kreski to P(A'UB) poprawnie zinterpretowałem?
16 kwi 20:24
jerey:
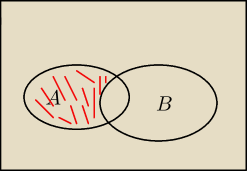
P(A\B')
16 kwi 20:25
zawodus: Nie
Część wspólna wypada
16 kwi 20:26
zawodus: Drugie też źle
16 kwi 20:26
jerey: nie ogarniam tego
16 kwi 20:28
bezendu:
a) źle !
(A'∪B)=1−P(A\B)
16 kwi 20:29
jerey: a P(A`) to wszystko z wyjątkiem A tak?
16 kwi 20:31
52: Tak
16 kwi 20:31
zawodus: Pierwsze było ok, moje przeoczenie
16 kwi 20:31
jerey: czyli P(A')=P(A'\UB)
16 kwi 20:33
zawodus: Co to jest
P(A'\∪B)?
16 kwi 20:35
jerey: sory, miałem na myśli P(A')=P(A'UB) *
16 kwi 20:37
zawodus: Nie
16 kwi 20:39
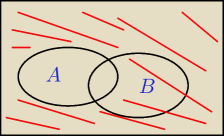
jerey: ok, dobra to zbiór A' wygląda tak? :
16 kwi 20:41
bezendu:
Zawodus moje rozpisanie jest źle ?
16 kwi 20:42
zawodus: A' to wszystko z wyjątkiem A
16 kwi 20:42
jerey:
16 kwi 20:42
zawodus: bezendu twoje jest ok
16 kwi 20:43
jerey:
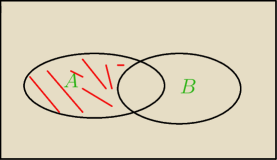
(A\B) tak?
16 kwi 20:45
bezendu:
To co teraz pytasz to podstawa... Jest ok.
16 kwi 20:48
jerey: chce to zrozumiec od podstaw, bo juz mi sie wszystko miesza
16 kwi 20:49
jerey: czyli w P(A'UB) nie moze byc czesci wspolnej AnB?
16 kwi 20:54
zawodus: Rozszerzenie nic nowego nie ma
Własności są na podstawie
16 kwi 20:55
bezendu:
Potrzebujesz okulary ?
20:29 i 20:43
16 kwi 20:55
zawodus: Tam jest część wspólna A∩B
Zacznij od zrozumienia pojęcia sumy zbiorów i iloczynu
16 kwi 20:57
jerey: to juz nie rozumiem,
o 20;26 zawodus napisałes ,ze bez czesci wspolnej:
o 20;31 napisałes ,ze było ok
o 20;43 napisałes ze rozwiązanie bezendu jest ok. czyli w koncu jak?
16 kwi 21:01
zawodus: Bo czytasz na wyrywki. Przeczytaj jeszcze post 20.31
16 kwi 21:03
jerey: no i co tam pisze?
16 kwi 21:10
zawodus: Jak mam ci przeczytać skoro nie usłyszysz?
16 kwi 21:11
jerey: no i w koncu sie nie dowiem,
wobec tego relacja P(A\B') jak wygląda? moglbys to zilustrowac?
16 kwi 21:15
bezendu:
P(A\B')=P(A∩B)
16 kwi 21:17
jerey: dziekuje
16 kwi 21:18
52:
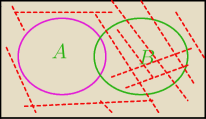
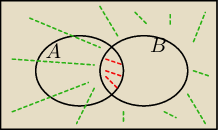zielono B'
czerwono A\B'
16 kwi 21:19
bezendu:
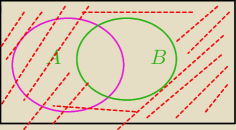
16 kwi 21:20
jerey: ok
16 kwi 21:29
jerey:
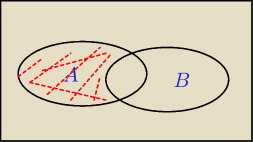
P(AnB') ?
17 kwi 09:36
52: Tak
17 kwi 09:50
jerey:
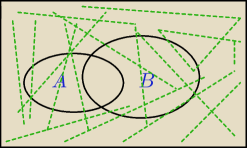
ok, P(A'uB') wszystko bez cz. wspolnej ?
17 kwi 10:10
52: Rysunek jest dobry (bez części wspólnej)
17 kwi 10:13
jerey:
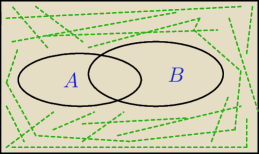
dobra, jeszcze jedno; P(A'nB')?
17 kwi 10:23
52: Tak
17 kwi 10:26
jerey: ok
17 kwi 10:29
jerey:
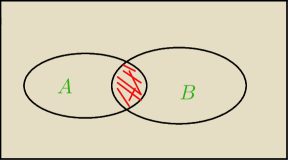
P((A'uB)nA))
17 kwi 11:38
bezendu:
przecież P(A'∪B)=1−P(A) więc ∅
17 kwi 12:05
17 kwi 12:09
Draghan: 11.38 jest wg mnie ok
17 kwi 12:24
52: 11:38 jest dobrze
17 kwi 13:08