Określ liczbę rozwiązań f(x) = m, jeśli f(x) = |x| + |x-2| kamczatka: Określ liczbę rozwiązań f(x) = m, jeśli f(x) = |x| + |x−2| −x − x +2 dla x∊ (−∞;0) f(x) = x − x ₂ dla x∊ <0;2) x + x − 2 dla x∊ <2;∞) x − 1 = 0 dla x∊ (−∞;0) f(x) = 2 dla x∊ <0;2) x = 1 dla x∊ <2;∞) coś mi to dziwnie wszystko powychodziło, jak to zrobić ?

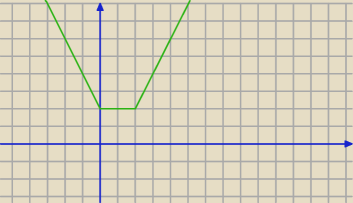
Radek: m∊(−∞,2) brak rozwiązań m∊{2} nieskończenie wiele rozwiązań m∊(2,∞) dwa rozwiązania

ZKS: Przecież −x − x + 2 = −2x + 2 a nie jak napisałeś x − 1? Skąd to wziąłeś?

ZKS: Radek po prostu zapisuj m = 2 zamiast m ∊ {2}.

kamczatka: to te moje obliczenia są dobre ? faktycznie będzie −2x+2 i 2x−2