Rozwiąż nierówność markopolo: Rozwiąż nierówność √x+4−x+2>0

zośka: zał x+4≥0 t=√x+4≥0 t²=x+4 x=t²−4 t−(t²−4)+2>0

zośka: czyli mamy nierówność: t²−t−6<0 i zał. t≥0 (t+2)(t−3)<0 i zał. t≥0 t∊<−2,3> i t≥0 , zatem 0≤t<3 0≤√x+4<3 x+4<9 x<5 oraz założenie x+4≥0 (czyli x≥−4) −4≤x<5

markopolo: Nie rozumiem a mozna to rozwiazac bez zmiennej pomocniczej?

markopolo: Mogłby ktoś mi to przedstawić w jeszcze jakis inny sposob?

wielomian: a można stronami do kwadratu podnieść wtedy pozbędziemy się pierwiastka

ZKS: Zaczynamy najpierw od dziedziny. x + 4 ≥ 0 ⇒ x ∊ [−4 ; ∞) √x + 4 − x + 2 > 0 √x + 4 > x − 2 Zauważamy że jeżeli prawa strona jest ujemna oraz argumenty należą do dziedziny to mamy rozwiązanie bo lewa strona jest nieujemna jako wartość z pierwiastka parzystego stopnia. x − 2 < 0 ⇒ x ∊ (−∞ ; 2) ∧ x ∊ [−4 ; ∞) ⇒ x ∊ [−4 ; 2) Dalej zakładamy że lewa strona jest nieujemna oraz argumenty należą do dziedziny i podnosimy obustronnie do kwadratu. x − 2 ≥ 0 ⇒ x ∊ [2 ; ∞) ∧ x ∊ [−4 ; ∞) ⇒ x ∊ [2 ; ∞) √x + 4 > x − 2 / ² (√x + 4)² > (x − 2)² x + 4 > x² − 4x + 4 x² − 5x < 0 x(x − 5) < 0 ⇒ x ∊ (0 ; 5) x ∊ (0 ; 5) ∧ x ∊ [2 ; ∞) ⇒ x ∊ [2 ; 5) Na sam koniec bierzemy sumę przypadków zatem x ∊ [−4 ; 2) ∨ x ∊ [2 ; 5) ⇒ x ∊ [−4 ; 5).

Mila: II sposób √x+4−x+2>0⇔ √x+4>x−2 D: x+4≥0⇔x≥−4 Lewa strona jest nieujemna z definicji pierwiastka kwadratowego. Badamy kiedy prawa jest nieujemna x−2≥0⇔x≥2 Zatem dla x∊<−4, 2) nierówność jest spełniona (lewa nieujemna, prawa ujemna) Dla x≥2 obie strony są nieujemne i możemy podnieść obustronnie do kwadratu x+4>x²−4x+4 x²−5x<0 x(x−5)<0 i x≥2 x>0 i x<5⇔2≤x<5 łącznie: −4≤x<5

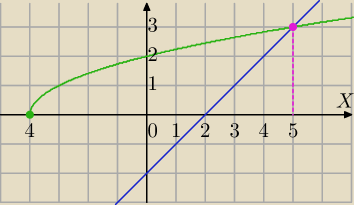
Mila: III sposób. √x+4>x−2⇔ wykres f(x)=√x+4 leży nad wykresem funkcji y=x−2 Metoda graficzna f(x)=√x+4, D: x≥−4 g(x)=x−2 Punkt przecięcia √x+4=x−2 i x∊D P(5,3) dla x≥−4 i x<5 wykres f(x) leży nad wykresem g(x)=x−2 odp. x∊<−4,5)

renata: rozwiąż nierówność 3−√18/4x≥√8x−1/5

Jerzy: Cześć Mila Nie szczepiłaś się przeciwko żółtatce ?

Eta: Nie musiała bo nie jest "żółta"Mila ... tylko Mila

Mila: Już nabrałam odporności, to było 4 lata temu