Janek191:
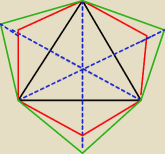
Czerwone odcinki − krawędzie pomiędzy którymi jest kat o mierze 120
o
− nie można zbudować ostrosłupa !
Zielone odcinki − krawędzie pomiędzy którymi jest kąt o mierze < 120
o
Bogdan:
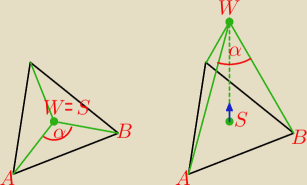
Wyobraźmy sobie, że ostrosłup wymieniony w zadaniu ma zerową wysokość, wówczas każda
ściana boczna leży na podstawie (czyli na trójkącie równobocznym) i wierzchołek W ostrosłupa
też leży na tej podstawie dokładnie punkcie S będącym środkiem okręgu opisanego na podstawie
i okręgu wpisanego w podstawę. Miara kąta α między krawędziami bocznymi jest równa jednej
trzeciej kąta pełnego, czyli 120
o.
Podnosimy punkt W nad podstawę tworząc ostrosłup prawidłowy. Co teraz dzieje się z miarą
kąta α, zwiększa się czy zmniejsza się? Pamiętamy, że jeśli punkt W leżał na podstawie
w punkcie S, to α = 120
o.
