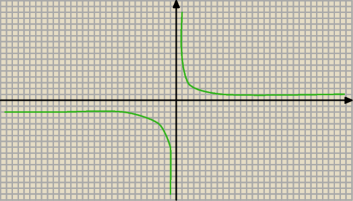
 Na podstawie zamieszczonego wykresu funkcji określ jej
własności:
a) dziedzina funkcji
b) zbiór wartości
c) miejsca zerowe
d) przedziały monotoniczności
e) zbiór argumentów, dla których funkcja przyjmuje
wartości dodatnie
f) zbiór argumentów, dla których funkcja przyjmuje
wartości większe od jeden
g) wartość maksymalna i minimalna
y=f(x)
Na podstawie zamieszczonego wykresu funkcji określ jej
własności:
a) dziedzina funkcji
b) zbiór wartości
c) miejsca zerowe
d) przedziały monotoniczności
e) zbiór argumentów, dla których funkcja przyjmuje
wartości dodatnie
f) zbiór argumentów, dla których funkcja przyjmuje
wartości większe od jeden
g) wartość maksymalna i minimalna
y=f(x)
 a) Dziedzina, czyli wszystkie argumenty, dla których funkcja f(x) ma sens. Mówiąc
łopatologicznie − wszystkie iksy funkcji. Czyli w tym przypadku x ∊ R \ {0}
Bo x = 0 jest asymptotą pionową funkcji.
b) Zbiór wartości, czyli wszystkie wartości, jakie przyjmuje funkcja. Czyli wszystkie jej
igreki. Również y ∊ R \ {0}
c) Czy ta funkcja posiada przecięcia z osiami ukł. współrzędnych? Jeśli tak, to jakie?
d) Dla jakich iksów funkcja maleje? Dla jakich iksów funkcja rośnie? Dla jakich jest stała?
e) dla jakich iksów wykres jest nad osią x?
f) dla jakich iksów funkcja jest nad kreską poziomą, przechodzącą przez y = 1?
g) Czy ta funkcja posiada minimum i maksimum? Jeśli tak, to jakie?
a) Dziedzina, czyli wszystkie argumenty, dla których funkcja f(x) ma sens. Mówiąc
łopatologicznie − wszystkie iksy funkcji. Czyli w tym przypadku x ∊ R \ {0}
Bo x = 0 jest asymptotą pionową funkcji.
b) Zbiór wartości, czyli wszystkie wartości, jakie przyjmuje funkcja. Czyli wszystkie jej
igreki. Również y ∊ R \ {0}
c) Czy ta funkcja posiada przecięcia z osiami ukł. współrzędnych? Jeśli tak, to jakie?
d) Dla jakich iksów funkcja maleje? Dla jakich iksów funkcja rośnie? Dla jakich jest stała?
e) dla jakich iksów wykres jest nad osią x?
f) dla jakich iksów funkcja jest nad kreską poziomą, przechodzącą przez y = 1?
g) Czy ta funkcja posiada minimum i maksimum? Jeśli tak, to jakie?
 Nick dobrałeś sobie wyborny
Nick dobrałeś sobie wyborny  Nie przejmuj się, chociaż należałoby się paru podstawowych pojęć douczyć
Nie przejmuj się, chociaż należałoby się paru podstawowych pojęć douczyć  Zaraz Ci rozpiszę
Zaraz Ci rozpiszę 
 tak, nik idealnie do mnie pasuje
tak, nik idealnie do mnie pasuje  wiem,że mam spore braki
wiem,że mam spore braki  sporo poprostu nie
rozumiem
sporo poprostu nie
rozumiem
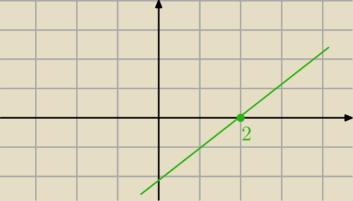 Spróbuj powiedzieć dla jakich x , ta funkcja przyjmuje wartości dodatnie ?
Spróbuj powiedzieć dla jakich x , ta funkcja przyjmuje wartości dodatnie ?


 Dla x = 2, y = 0. A 0 nie jest dodatnie
Dla x = 2, y = 0. A 0 nie jest dodatnie 


| 1 | ||
Intryguje mnie, skąd wziałeś w odpowiedzi f) : x = | ? | |
| 4 |

 Czy mogę wrzucić już rozwiązanie? Bo ja mogę poczekać,
aż wyłożysz wszystko, co wyłożyć chcesz
Czy mogę wrzucić już rozwiązanie? Bo ja mogę poczekać,
aż wyłożysz wszystko, co wyłożyć chcesz 

 To, co napisałeś Ty i to, co napisałem ja,
to są tylko takie zamienniki
To, co napisałeś Ty i to, co napisałem ja,
to są tylko takie zamienniki  c) oczywiście że nie ma
c) oczywiście że nie ma  d) jesteś na dobrym tropie, coś gdzieś piszczy, ale nie.
Ta funkcja jest przedziałami monotoniczna. Ty napisałeś, że dla x ∊ (−oo; + oo). Trochę się to
mija z prawdą, ponieważ:
1. funkcja nie istnieje dla x = 0
2. Funkcja nie maleje cały czas. Jeśli by tak było, to dla x = −1 wartość byłaby większa, niż
dla x = 1. A tak nie jest.
Ta funkcja maleje dla przedziałów (−oo; 0) i dla (0; +oo).
Zauważ, że nie napisałem (−oo;+oo) \ {0}, ani (−oo; 0) u (0; +oo). Tutaj mamy tak jakby dwa
różne przypadki, w których ta funkcja maleje.
e) patrzysz na wykres. Powyżej osi x funkcja ma dodatnie igreki. Musisz odczytać teraz, dla
jakich dokładnie iksów tak się dzieje.
Dla x ∊ (0; +oo).
f) Nie wiem, co wychodzi, bo nie ma skali na wykresie
d) jesteś na dobrym tropie, coś gdzieś piszczy, ale nie.
Ta funkcja jest przedziałami monotoniczna. Ty napisałeś, że dla x ∊ (−oo; + oo). Trochę się to
mija z prawdą, ponieważ:
1. funkcja nie istnieje dla x = 0
2. Funkcja nie maleje cały czas. Jeśli by tak było, to dla x = −1 wartość byłaby większa, niż
dla x = 1. A tak nie jest.
Ta funkcja maleje dla przedziałów (−oo; 0) i dla (0; +oo).
Zauważ, że nie napisałem (−oo;+oo) \ {0}, ani (−oo; 0) u (0; +oo). Tutaj mamy tak jakby dwa
różne przypadki, w których ta funkcja maleje.
e) patrzysz na wykres. Powyżej osi x funkcja ma dodatnie igreki. Musisz odczytać teraz, dla
jakich dokładnie iksów tak się dzieje.
Dla x ∊ (0; +oo).
f) Nie wiem, co wychodzi, bo nie ma skali na wykresie  Tu musisz sam do tego dojść
Tu musisz sam do tego dojść  Ale to
Ale to
| 1 | ||
ma być również być przedział. Prawdopodobnie x ∊ (0 ; | )  | |
| 4 |






 Co do "e", to nie wiem. Wartości większe od jeden miały być w f), a nie w e)...
Co do "e", to nie wiem. Wartości większe od jeden miały być w f), a nie w e)...  Odpowiedź do e) podałem poprawną
Odpowiedź do e) podałem poprawną  A do f) nie mogę precyzyjnie określić na podstawie wykresu, na którym nie ma zaznaczonych
wartości
A do f) nie mogę precyzyjnie określić na podstawie wykresu, na którym nie ma zaznaczonych
wartości  Owszem, J
Owszem, J  To było nieprecyzyjne. Ale chciałem wszystko rozpisać bardziej obrazowo, niż
precyzyjnie, żeby chłopak załapał
To było nieprecyzyjne. Ale chciałem wszystko rozpisać bardziej obrazowo, niż
precyzyjnie, żeby chłopak załapał 

