tryginometria
pooomocy: | | 2√5 | | tgα | |
jeśli kąt α jest ostry i sinα= |
| to wartość wyrażenia |
| jest równa |
| | 5 | | cosα | |
15 kwi 21:51
pooomocy: pomoże ktoś?
15 kwi 22:07
Darth Mazut: Narysuj trójkąt prostokątny, znajdź 3 bok, zauważ że tg/cos = sinα/cos2α
15 kwi 22:10
Darth Mazut: chociaż tego przekształcenia tryg nawet nie trzeba w sumie
15 kwi 22:10
pigor: ..., oj
, no to np. tak :
| tgα | | sinα | | sinα | |
| = |
| = |
| = |
| cosα | | cos2α | | 1−sin2α | |
| | 15*2√5 | | 2√5 | |
= |
| = |
| = 2√5 − ...  |
| | 1−45 | | 5−4 | |
15 kwi 22:12
pooomocy: dziękuje
15 kwi 22:15
Eta:
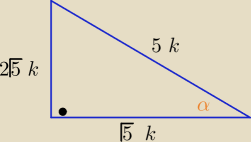
15 kwi 22:16
Dziadek Mróz:
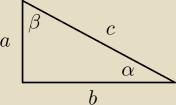
a = 2
√5
c = 5
| tg(α) | | | | sin(α) | | 1 | |
| = |
| = |
| * |
| = |
| cos(α) | | cos(α) | | cos(α) | | cos(α) | |
| | sin(α) | |
= |
| = (a) ... |
| | cos2(α) | |
sin
2(x) + cos
2(x) = 1
cos
2(x) = 1 − sin
2(x)
| | sin(α) | |
... (a) = |
| = ... |
| | 1 − sin2(α) | |
Teraz to z górki
15 kwi 22:16
Eta:
Raczej "pod górkę"
15 kwi 22:17
pooomocy: =..? Niestety faktycznie pod górkę :x
16 kwi 09:52
J: Przecież masz podane rozwiązanie ...post: 22:16 od "Eta"
16 kwi 10:04
Dziadek Mróz:
Jeżeli
i
sin(α) = x
to
| sin(α) | | x | | | |
| = |
| = |
| = ... |
| 1 − sin(α) | | 1 − x | | | |
16 kwi 10:16