Ostrosłup
Mateusz: Podstawą ostrosłupa ABCD jest trójkąt równoramienny ABCD, w którym |AB|=|AC|=7, |BC|=6.
Krawędzie boczne mają długości |DA|=7, |DB|=|DC|=5. Oblicz objętość tego ostrosłupa.
15 kwi 21:11
pigor: ...,
Vo= 13 P
ΔDBC*
13*
12*6*4*H=
4H= ?, gdzie
H − wysokość ostroslupa, no to niech R promień okręgu
opisanego na ΔDBC, to z
2,5R=
45 ⇒ 4R=12,5 ⇔ 8R=25 ⇒ R=
258, wtedy
H
2=7
2− R
2= 7
2−(
258)
2= (7−3
18)(7+3
18)= 3
78*10
18=
=
318*
818= (
98)
2*31 ⇒
H=98√31 , zatem
Vo= 4*
98√31=
92√31=
4,5√31 − szukana objętość w j
3. ...
15 kwi 21:47
Eta:
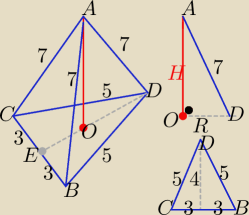
Rys. do rozwiązania podanego przez
pigora
15 kwi 22:00
pigor: ...o
jak ślicznie; ja dziękuję i chowam
...
bez pytania do swojej " szuflady". ...
15 kwi 22:07
Eta:
15 kwi 22:08