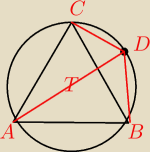
ma ktoś pomysł ? dyzio: Nie mogę poradzić sobie z zadaniem jeśli ktoś mógłby pomóc. W okrąg wpisano trójkąt równoboczny ABC. Na okręgu wybrano punkt D (różny od punktów A, B, C) i poprowadzono trzy odcinki DA, DB, DC. Wykaż, że suma długości dwóch krótszych odcinków jest równa długości odcinka trzeciego.

bezendu: w ptolemeusza może ?

dyzio: A inny sposób ? Nie przychodzi Ci do głowy ? Tego twierdzenia nie braliśmy i nie ma go w podręczniku.

bezendu: Przychodzi i zaraz napisze

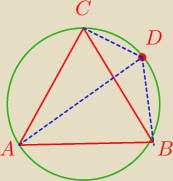
bezendu: Trójkąt ABD oraz trójkąt ADC są trójkątami prostokątnymi i |AB|=|AC|=|BC|=x DB=y CD=z AD=k Z twierdzenia pitagorasa mam: x²+y²=k² x²+z²=k² 2x²+z²+y²=2k² z²+y²=2k²−2x² z²+y²=2(k²−x²) coś w tym stylu ale dalej się zaciąłem ?

bezendu: Nie no to jest Twierdzenie ptolemeusza i ja przy tym zostaje !

zawodus: Trójkąt ABD nie jest prostokątny

Alfa: przecież trójkąt ABD, czy ADC nie jest prostokątny (tzn może być, jeśli AD będzie średnicą okręgu, ale my tego zakładać nie możemy), nie możemy więc stosować tw. Pitagorasa.

dyzio: Już dzisiaj za dużo zadań z matmy zrobiłem i czuje, że czas na odpoczynek Jutro rano siadne do zadania, może dam rade. Jakbyś miał jakiś mały pomysł to możesz się z nim podzielić, nie wzgardzę

bezendu: Czyli zostaje tw ptolemeusza. Pierwsza myśl najlepsza !

zawodus: Jeśli zadanie pochodzi z arkusza maturalnego to da się je wykonać bez twierdzenia Ptolemeusza, którego nie ma w programie LO

dyzio: zadanie pochodzi ze zbioru zadań z nowej podstawy programowej do liceum i technikum

dyzio: więc raczej da się je rozwiązać innym sposobem, ale zadanie dla ambitnych.

Alfa: ∡ACB = ∡ADB = 60^o −−> kąty wpisane w okrąg oparte na tym samym łuku ∡ADC = ∡ABC = 60^o −−> − || − − || − − || − − || − z tw. cosinusów:(trzymając się oznaczeń @bezendu) x² = y² + k² − 2ykcos60^o (w ΔABD) x² = z² + k² − 2zkcos60^o (w ΔADC) więc: y² + k² − 2ykcos60^o = z² + k² − 2zkcos60^o dokończ

dyzio: ok, dzięki !

zawodus: ciekawe zadanko

dyzio: w tych książkach jest ich więcej niektóre łatwe nie są.

dyzio: Jeśli by kogoś interesowało, albo ktoś miałby problem z tym zadaniem z poprzednim sposobem, mam takie rozwiązanie.

	sin(60 − ∠BCD)		sin∠BCD)
|CD| + |DB| = |AD|		+ |AD|		=
	sin(60 + ∠BCD)		sin(120 − ∠BCD)

|AD|(..) te przekształcenia wynikają z tw. sinusów dla trójkątów odpowiednio: ACD i ABD. A teraz już tylko ze wzorów redukcyjnych pokazujesz, że ten nawias jest równy 1.