? Damo93: Dla jakich wartości parametru m pierwiastki równania x² −2mx −m −2 = 0 są zawarte między liczbami −2 i 4 ? W podpowiedzi mam zapisane takie warunki: Δ > 0, f(−2) >0, f(4) >0 i −2<X_w< 4 Nie rozumiem tego do końca, czy mógł by mi to ktoś wyjaśnić dokładniej ? z góry dziękuję.

Marcin: Δ>0, żeby były dwa różnie pierwiastki. x_w jest po to, żeby wierzchołek paraboli był zawarty pomiędzy tymi miejscami zerowymi.

ZKS: Te podpowiedzi to rozwiązania może by powiedzieć.

Piotr 10: a nie przypadek Δ ≥ 0 ZKS ?

Marcin:

	b
ZKS trzeba jeszcze wiedzieć, że xw= −		. Nie ma tak łatwo
	2a

ZKS: Na maturze tak Δ ≥ 0.

Damo93: ZKS no tak ale nie potrafię sobie tego jakoś zobrazować

Piotr 10: Ok, a w rzeczywistości Δ > 0

Marcin: znowu problem z pierwiastkami W sumie powinno być, że pierwiastki mają być różne. Ale jak już miałeś taką podpowiedź, to tego nie negowałem

ZKS: Trzeba również wiedzieć że Δ = b² − 4ac.

Eta:

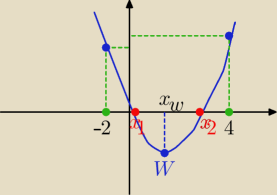
ZKS: Po takim rysunku powinieneś już wiedzieć dlaczego takie warunki.

Technik: Właśnie ja też się dopytam czemu takie warunki ?

Damo93: wszystko jasne dziękuje

Marcin: No bo kto wytłumaczy jak nie Eta

Eta: oczywiście, Δ≥0 bo wierzchołek W może też należeć do osi OX

Technik: Ja tez już zrozumiałem po rysunku kochanej Ety

ZKS: f(−2) > 0 oraz f(4) > 0 jest po to (jaki widać z rysunku) aby te pierwiastki znajdowały się w przedziale (−2 ; 4). Jeżeli f(−2) < 0 (tutaj a > 0 więc ramiona paraboli skierowane do góry) to wartość tej funkcji była by ujemna a dla miejsca zerowego wartość jest równa 0 zatem ten jeden z pierwiastków nie byłby zawarty w przedziale (−2 ; 4). Jeżeli dalej nie jest jasne pisać.

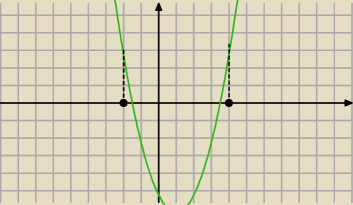
...: z rysunku zobaczysz dlaczego f(−2)>0 i f(4)>0

ZKS: Widzę że nie potrzebnie pisałem. Za ładny rysunek zrobiłaś Eta i wszystko już wiedzą.

Technik: Dzięki ZKS wszystko jasne !

ZKS:

nauczycielka: Bo was w szkole powinni uczyć rysunek to podstawa Cześć wszystkim

ZKS: Dobry wieczór.