napisz równania stycznych Matejko: napisz równania stycznych do okręgu (x−1)²+(y−1)²=4 poprowadzonych z punktu A(3;5) moge zacząć od wyznaczenia prostej jako y=a(x+2)?

J: A skąd ta prosta ?

Matejko: http://www.zadania.info/d1430/1663450

Matejko: robiłem adekwatnie do tego zadania

J: To nie rób adekwatnie ... bo tam punkt jest specyficzny. y = ax + b 5 = 3a + b ⇔ b = 5 − 3a y = ax + 5 −3a ⇔ y = a(x −3) + 5 − równanie pęku prostych przechodzących przez A.

Matejko: ok to liczę dalej mógłbyś też policzyć to zadanie i powiedzieć mi później czy odpowiedź jest dobra?

J: Nie mam do tego cierpliwości ... , ale pewnie ktos na FORUM sprawdzi ..

Matejko: wyszło mi że a=³₄ robiłem to z odległości środka od prostej

Matejko: dlaczego tylko 1 a mi wyszło?

Matejko: widać że jedna prosta to x=3 ale jak to policzyć?

Matejko:

WK: Matejko dobrze Ci wyszło niby proste zadanie a jednak sie czasami zapomina

Matejko: a jak wyznaczyć to x=3

Technik: Nie wiem co Ty tworzysz ? Umiesz wgl wyznaczać styczne do okręgu ? Zobacz post @J A potem skorzystaj ze wzoru na odległość punktu od prostej..

Matejko: Technik.. mam wyznaczoną prostą ale z tego wychodzi tylko 1 prasta i to nie liczy prostej x=3... pytam jak ta prostą policzyć tą x=3

Technik: masz prostą postaci y=ax+b wstaw za a to zobaczysz.

Matejko: ale z tego i tak nie wyznacze x=3 tylko ³₄(x−3)+5

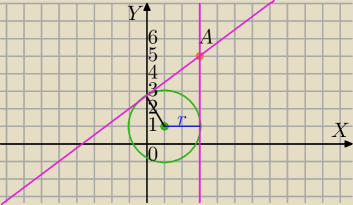
Mila: s: y=ax+b i A∊s⇔5=3a+b, b=5−3a s: y=ax+5−3a 1) możesz to podstawić do równania okręgu i wyznaczyć a, tak aby równanie miało jedno rozwiązanie (Δ=0) albo jedna styczna : x=3 druga styczna: przekształcamy równanie stycznej s:ax−y+5−3a=0 postac ogólna korzystamy z tego , że odległość stycznej od środka okręgu jest równa promieniowi S(1,1) , r=2

	|a*1−1+5−3a|
d=		=2
	√a2+1

⇔|4−2a|=2√a²+1 /:2 |2−a|=√a²+1 /² 4−4a+a²=a²+1 3−4a=0 4a=3

	3
a=
	4

	3		9		11
b=5−3*		=5−		=
	4		4		4

	3		11
s: y=		x+
	4		4

Matejko: czyli jakby takie zadanie było na maturze to mam napisać że 2 styczna to x=3 co wynika z rysunku?

Mila: Z warunków zadania.

WK: Mila mogłabyś zrobic sposobem podstawienia do wzoru okręgu? Próbuje Próbuje i cos mi nie wychodzi.....

Mila: WK, nie próbuj, duzy stopień komplikacji w tym przypadku, szkoda czasu. wychodzi rozwiązac takie równanie: (8a−6a²−2)²−4(13−24a+9a²)*(1+a²)=0

	3
a=
	4

Łatwiej znaleźć punkty styczności. Jeśli znasz konstrukcję stycznej to ładnie wychodzi.

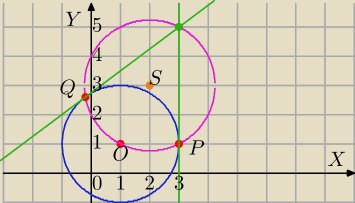
Mila: 1) Jeden punkt styczności odczytujesz, drugi z symetrii względem prostej przechodządcej prze A i środek okręgu. Albo 2) Metoda geometryczna wyznaczenia punktów styczności

	1+3		1+5
S=(		,		)=(2,3)
	2		2

R=|SA|=√5 (x−2)²+(y−3)²=5 (x−1)²+(y−1)2=4 po rozwiązaniu: punkty przecięcia okręgów ( punkty styczności)

	−1		13
P=(3,1), Q=(		,		)
	5		5

Prosta : AP to x=3 =================== Prosta: AQ 5=3a+b

13		1
	=−		a+b
5		5

	13		1
5−		=3a+		a
	5		5

12		16
	=		a
5		5

	12		5
a=		*
	5		16

	3
a=
	4

	11
b=
	4

	3		11
y=		x+
	4		5

====================