Trójkąty, trójkąciki... Draghan: Podstawa AB trójkąta równoramiennego ABC ma długość 8 oraz kąt BAC = 30^o. Oblicz długość środkowej tego trójkąta. Zadanie maturalne, maj 2011. http://vpx.pl/i/2014/04/15/trójkąty_zadanie.png Ja widzę treść polecenia, jako trójkąt I. Aby obliczyć środkową, czyli d, skorzystam z tw. cosinusów dla trójkąta III. Brakuje mi wartości x.

	1
Wartość x to		ramienia trójkąta ABC oraz trójkąta AHC, który jest trójkątem o
	2

kątach 30, 60, 90, o dłuższej przyprostokątnej równej 4. Widać to na trójkącie II.

	16√3
Z zależności boków w takim trójkącie, wychodzi mi, że y =		, a więc x =
	3

	8√3
		.
	3

A kiedy zastosuję tw. cosinusów do trójkąta III, podstawiając wyliczonego x, wychodzi mi... d = x Najgorsze jest to, że nie mam pojęcia, w którym miejscu mojego rozwiązania jest błąd Moje pytanie numer jeden: czy oparłem moje obliczenia na dobrych warunkach? Tj. czy wszystkie rysunki są poprawne?

Draghan: Chyba widzę mój błąd (rachunkowy). Ale jeszcze muszę się upewnić. Wracam do obliczeń... Ale moje pytanko nadal "jest w grze"

Draghan: Heh. Źle użyłem własności trójkąta 30,60,90 Jeden z jego boków ma długość a√3, a ja

	a√3
wstawiałem
	2

Ale i tak coś mi się nie zgadza Wracam do liczenia.

razor: nie uzywaj wlasnosci trojkata 30,60,90 bo wtedy mozna sie latwo pomylic przynajmniej ja sie czesto mylilem. latwiej jest uzyc funkcji trygonometrycznych

Bogdan:

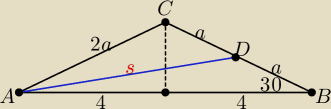
4		2		√3		4
	= cos30o ⇒		=		⇒ a =
2a		a		2		√3

Z twierdzenia cosinusów w trójkącie ABD: s² =...

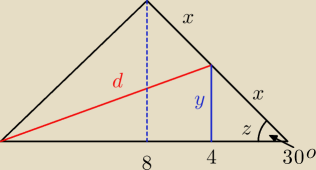
Trivial: Rysunki wyglądają na poprawne. Ja mam inny sposób, który prowadzi do równań:

	4
2xcos(30o) = 4 → x =
	√3

	2
y = xsin(30o) =
	√3

z = xcos(30^o) = 2

	4
d2 = (8−z)2 + y2 = 36 +
	3

Draghan: Już wszystko jasne. Sposób rozwiązania miałem poprawny, ale obliczenia się położyły. To znaczy skopałem do kwadratu w jakichś trzech miejscach Dziękuję Sposób Bogdana wykorzystałbym w przypadku, gdyby trójkąt ACH (gdzie H to punkt przecięcia wysokości z podstawą trójkąta ABC) nie był jednym z tych charakterystycznych

Draghan: Czekaj, Trivial, bo nie łapię jednego. Pierwsza linijka Skąd wynika? Ogólnie Twój sposób również szybciutki i łatwy w użyciu, ale skąd ta pierwsza linijka?

Trivial: Z tego trójkąta z linią przerywaną.

Draghan: A. No tak Dla Was po