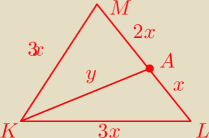
problem bezendu: na boku trójkąta równobocznego KLM wybrano punkt taki a, że AM:AL=2:1 wyznacz sin kąta LKA y²=x²+(3x)²−2*x*3x*cos60⁰ y²=10x²−3x² y²=7x² y=√7x x²=(√7x)²+(3x)²−2*3x*√7x*cosα x²=7x²+9x²−6√7cosαx² −15x²=−6√7x²cosα

	5√7
cosα=
	14

sinα=U{√21{14} W książce inny wynik ?

bezendu:

	√21
sinα=		tak mi wyszło.
	14

Janek191: Wygląda, że dobrze wyszło

bezendu: To chyba błąd w arkuszu. Dziękuję

Saizou : jał wychodzą mi dwa 'y' w ΔKMA

	1
y2=(3x)2+(2x)2−2*3x*2x*
	2

y²=4x² y=2x w Δ AKL

	1
y2=(3x)2+x2−2*3x*x*
	2

y²=7x² y=x√7

Bogdan:

	x		y
Z twierdzenia sinusów:		=
	sin(∡LKA)		sin60o

Mila: Dobrze. Podobne zadanie już rozwiązywaliśmy.

bezendu: Dziękuję, za odpowiedzi, chciałem się upewnić bo w arkuszu było inaczej.

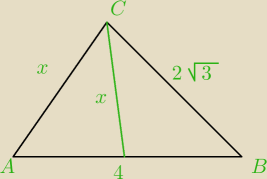
bezendu: Środkowa trójkąta ABC jest równa bokowi AC. Wyznacz kąty trójkąta ABC wiedząc, że |AB|=4 BC+2√3

1
	√2*(2√3)2+2x2−42=x /2
2

1
	(8+2x2)=x2
4

	1
2+		x2=x2/2
	2

4+x²=2x² 4=x² x=4 I teraz z tw cos ? Wiem, że można jeszcze z przyrównania ale czy ten sposób jest ok ?

Saizou : dlaczego wyszły nam dwa różne "y"

bezendu: ?

bezendu: Wysokość poprowadzona z wierzchołka C ma długość h. Kąty BAC i ABC są ostre i mają odpowiednio miaty α i β oblicz obwód trójkąta

	h		h		h(cosβsinα+cosαsinβ)
Obw=		+		+		?
	sinα		sinβ		sinαsinβ

bezendu: ?

bezendu: ?

Mila: No i co z tym zadaniem 22:11? x=2 h=√3 tam masz Δ równoramienny o ramionach x.

bezendu: Tam, wiem jak wyliczyć kąty. Ale 22:21 ?

Saizou : ale po co liczyć kąty skoro są one dane ? z funkcji sinus i tangens xd

bezendu: Mówisz o zadaniu 22:21 ?

Saizou : tak xd

Eta: 22:21 jest ok

bezendu: Dziękuję o to mi chodziło

Mila: Dobrze, ostatni ułamek zapisz :

h*sin(α+β)
sinα*sinβ

	sinα+sinβ+sin(α+β)
Obw.=h*
	sinα*sinβ

bezendu: Dziękuję. I dziś jestem zadowolony z postępów

Eta: Ja też bo już czekam tylko na "zajączka"

Technik: Zajączek to super ''gościu''

bezendu: A ja nawet nie dopuszczam myśli, że to już niedługo...

Eta: podobnie jak Technik

Technik: Eta pamiętasz tę dowody ? Podszkolisz mnie z prawdopodbieństwa ? Działania na zbiorach, nierówności ? Wykładowcy przymykają teraz oko na mnie w okresie maja i kwietnia więc mam jeszcze więcej czasu na naukę do matury

Eta: Pamiętasz "wierszyk" ?

Technik: Oczywiście ! Nawet nie wiesz ile ten wierszyk mi pomógł

Eta: To teraz "trenuj" zadania z prawdopodobieństwa

Technik: Przeważnie są kostki, poszukam sobie i jutro Cię będę szukał na forum

Draghan: Wierszyk? Jaki wierszyk?