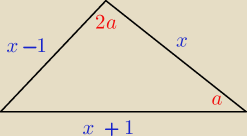
? Damo93: Zad.7.Pazdro Długości boków pewnego trójkąta wyrażają się kolejnymi liczbami naturalnymi. Największy kąt w tym trójkącie jest dwa razy większy od kąta najmniejszego. wyznacz długości boków tego trójkąta. Zrobiłem taki rysunek i : z tw. sinusów

x+1		x−1
	=
sin2α		sinα

sin2α(x−1)= sinα(x +1) sin2α=2sinαcosα 2sinαcosα(x−1) = sinα(x+1) / sinα 2cosα(x−1)= x+1

	x+1
więc cosα =
	2x−2

dalej z tw. cos.

	x+2
W odp. cosα=		Co robię nie tak ?
	2x

Damo93: oni chyba inaczej oznaczyli boki jako x, x+1,x +2 −−> ale i tam mam coś zle bo inne długości mi wychodzą

Janek191: Pewnie długości boków oznaczono przez: x , x + 1, x + 2

bezendu:

n+2		n
	=
sin2α		sinα

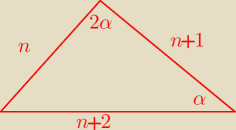
(n+2)sinα=nsin2α sinα(n+2)=2nsinαcosα

	n+2
cosα=
	2n

	n+2
n2=(n+1)2+(n+2)2−2[(n+1)(n+2)*		]
	2n

	n3+5n2+8n+4
n2=2n2+6n+52−2(		)
	2n

n²−3n−4=0 n=4 długości boków,4,5,6

PW: Rozwiązanie nie może zależeć od oznaczeń − długości boków w obu sposobach będą jednakowe. Wyliczyłeś

	x+1
2cosα =		,
	x−2

zatem z twierdzenia kosinusów

	x+1
(x−1)2 = x2+(x+1)2 − x(x+1)
	x−2

− do rozwiązania równanie 3. stopnia.

Damo93: właśnie tak teraz policzyłem ale nie wiem dlaczego nie wyszło przy oznaczeniu boków jaki x−1,x,x+1

Damo93: PW zapewne popełniłem gdzieś błąd w obliczeniach

zawodus: Był błąd w rachunkach

Damo93: dobra lecimy dalej bo maturka tuż tuż a ja się nadal mylę Dzięki za odp. !