plani
jerey:
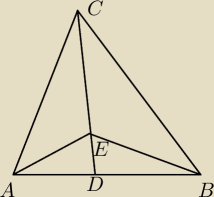
Na boku AB trójkąta ABC wybrano punkt D , a na odcinku CD wybrano punkt E . Wykaż, że
stosunek pól trójkątów AEC i BEC jest równy stosunkowi pól trójkątów ADC i BDC .
zadanie z VII matury z zadania info
zrobił je ktos?
13 kwi 21:20
Marcin: No ale chyba nie z tej wczorajszej VII, co nie?

13 kwi 21:22
jerey: nie, to nie z wczorajszej

13 kwi 21:23
jerey: zrobiłes to Marcin?
13 kwi 21:23
Marcin: Szczerze mówiąc, to nie robiłem tej maturki. Teraz w sumie wziąłem się za inną, ale mogę Ci
podać mniej więcej odpowiedź

13 kwi 21:25
Saizou :
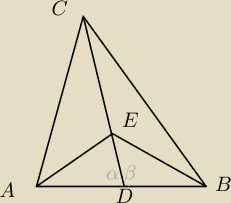
podpowiem że z pól wychodzi bardzo przyjemnie xd
13 kwi 21:32
Eta:

| | 1 | | 1 | |
P(ADC)}= |
| x*h , P(DBC)= |
| y*h |
| | 2 | | 2 | |
| | 1 | | 1 | |
P(AEC)= |
| x*(h−w) , P(BEC)= |
| y(h−w) , w∊(0,h) |
| | 2 | | 2 | |
13 kwi 21:47
jerey: a kąty AEC, CEB BEA będą takie same?
13 kwi 21:48
Eta:

13 kwi 21:50
Saizou : mówiłem że z pól xd

13 kwi 21:51
jerey: dobra, dzieki wam, ale na dowodach z planimetrii to polegne ma maturze .
13 kwi 21:52
Eta:

13 kwi 21:52
Saizou : tylko że ja przechodziłem trochę inaczej ale to samo wyszło xd
| | 1 | |
po wziąłem wzór |
| absinα, ważne że wyszło to samo  |
| | 2 | |
13 kwi 21:54
aga: nie rozumiem czemu P(AEC)=(1/2)x*(h−w), wytlumaczy mi ktos?
21 kwi 22:14
Eta:
| | 1 | | 1 | | 1 | |
P(AEC)=P(ADC)−P(ADE)= |
| *x*h − |
| *x*w= |
| x*(h−w) |
| | 2 | | 2 | | 2 | |
22 kwi 00:10
 Na boku AB trójkąta ABC wybrano punkt D , a na odcinku CD wybrano punkt E . Wykaż, że
stosunek pól trójkątów AEC i BEC jest równy stosunkowi pól trójkątów ADC i BDC .
zadanie z VII matury z zadania info
zrobił je ktos?
Na boku AB trójkąta ABC wybrano punkt D , a na odcinku CD wybrano punkt E . Wykaż, że
stosunek pól trójkątów AEC i BEC jest równy stosunkowi pól trójkątów ADC i BDC .
zadanie z VII matury z zadania info
zrobił je ktos?



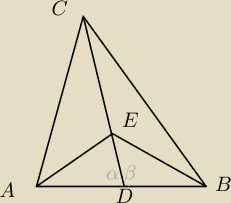 podpowiem że z pól wychodzi bardzo przyjemnie xd
podpowiem że z pól wychodzi bardzo przyjemnie xd




