Funkcja kwadratowa, funkcja liniowa, funkcja trygonometryczna Oliwia: 1. Wyznacz współczynniki a, b i c funkcji kwadratowej wiedząc, że f(−3)=f(−1)=−3 oraz, że ma ona jedno miejsce zerowe. 2. Znajdź wzór funkcji liniowej, której wykres przechodzi przez punkt B i jest prostopadły do prostej k. B=(−2,4), k: 3x+2y−1=0 3. Oblicz sinα, tgα gdy cosα = 3/5 wiedząc, że α jest kątem ostrym

5-latek:

	sinα
3) sinα=√1−cos2α tgα=
	cosα

Piotr: 1) {−3=9a−3b+c {−3=a−b+c {b²−4ac=0 rozwiaz uklad rownan

Piotr: 2)

	3		1
k: y= −		x +
	2		2

a₁*a₂ = −1 to warunek prostopadlosci prostych wyznacz a i podstaw punkt

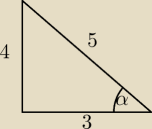
Piotr: 3) teraz juz wszystko mozesz wyznaczyc

Eta:

	−3−1
1/ Osią symetrii paraboli jest prosta x=xw to xw=		= −2
	2

funkcja ma jedno miejsce zerowe,to: y=a(x−x_w)² ⇒ y=a(x+2)² i f(−3)=−3 to: −3=a(−3+2)² ⇒ a=−3 y=−3(x+2)²

Piotr: troche szybciej

Eta: