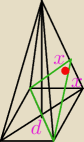
cos między ścianami bocznymi mrb: Oblicz cosinus kąta zawartego między ścianami bocznymi ostrosłupa prawidłowego czworokątnego, którego ściany boczne są trójkątami równoramiennymi o ramieniu dwa razy dłuższym od krawędzi podstawy. No to zaczynam: z trójkąta równoramiennego liczę sobie jego pole, otrzymuję:

	√15 a2
PΔ =
	4

Potem liczę wysokość (x) opuszczoną na podstawę 2a w ścianie bocznej, otrzymuję:

	√15 a
x =
	8

I teraz stosuję tw. cosinusów dla kąta między ścianami bocznymi (x,x,a√2) i otrzymuję cosα > 1 Co robię nie tak?

bezendu:

	1
cosα=−
	15

mrb: no taka jest odpowiedź, ale skąd się to bierze? co tu robię źle?

dero2005:

	a
x =		√15
	4

mrb: Czemu taki x a nie taki jak u mnie?

Rafał28: Rozważ ponownie pole ściany bocznej w zależności od dwóch wysokości.

mrb: Jakoś tego nie widzę Mógłby może ktoś z Was rozrysować?

dero2005:

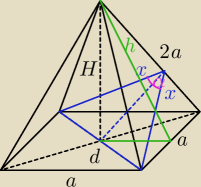
	a
h = √(2a)2 − (a2)2 =		√15
	2

x*2a = a*h

	a*h		a
x =		=		√15
	2a		4

d = a√2 d² = 2x² − 2x²cosα 2a² = 2x² − 2x²cosα x²cosα = x² − a²

	a2
cosα = 1 −
	x2

	1
cosα = −
	15