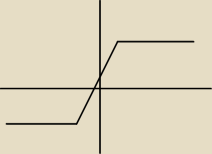
Dla jakiej wartości parametru p funkcja f(x) = |x + 2| + |1 - x| ma dokładnie dw drzewo: Dla jakiej wartości parametru p funkcja f(x) = |x + 2| + |1 − x| ma dokładnie dwa rozwiązania jeśli f(x) = p. −x − 2 − 1 + x dla x∊ (−∞;−2) f(x) = x + 2 − 1 + x dla x∊ <−2;1) x + 2 + 1 − x dla x∊ <1;∞) −3 dla x∊ (−∞;−2) f(x) = 2x+1 dla x∊ <−2;1) 3 dla x∊ <1;∞) coś mi tu nie tak wychodzi bo nigdzie nie ma 2 rozwiązań (rysunek u góry) według moich rozwiązań. co jest nie tak ?

ICSP: źle rozpisane przedziały dla x < −2 mamy (1 − x) > 0 zatem |1 − x| = 1 − x a nie −(1 − x) jak napisałeś. Dalej powtarzasz ten błąd.

ICSP: Dam Ci również pewna wskazówkę do zadań z wartością bezwzględna. Gdy masz coś np |1 − x| zapisz to sobie równoważnie jako |x−1|. Zdecydowanie łatwiej się liczy.

drzewo: dobra dzięki teraz wyszło wszystko ok.