analityczna Radek: W trójkącie ABC , gdzie |AC | = 2|AB | dane są B = (− 6,6) i C = (− 10,− 9) . Wyznacz współrzędne wierzchołka A , jeżeli leży on na prostej 3y + x = 1 robię te ze wzoru na długość odcinka ale nie wychodzi

sushi_ gg6397228: zapisz swoje obliczenia

Radek:

	1		1		1		1
(x+10)2+(−		x+		+9)2=4[(x+6)2+(−		x+		−6)2]
	3		3		3		3

sushi_ gg6397228: to liczymy dalej przyda sie pogladowy rysunek

Radek: Ale właśnie z tego nie wychodzi i trzeba inaczej tylko czemu ? Podniosłem obustronnie do kwadratu

Eta: Zapisz tak (będzie łatwiej liczyć) A(1−3y, y)

Marcin: Nie może nie wychodzić

Marcin: To będą dwie możliwość. Jedna to A=(−2;1). Może gdzieś się w obliczeniach ryjesz?

Radek: Już wyszło poprawnie

Marcin: Obliczenia?

Radek: \tak

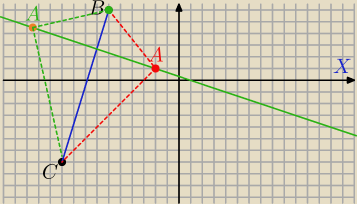
Mila: B = (− 6,6) i C = (− 10,− 9) 3y + x = 1 3y=−x+1

	−1		1
y=		x+
	3		3

|AC|=2|AB|

	−1		1
A=(x,		x+		)
	3		3

Licz długości |AC| i |AB|

Radek: A mogła by Pani dać mi jeszcze wskazówki do 10 zadań ?

Mila: Naturalnie. Skończyłeś to zadanie? Łatwiej liczyć na współrzędnych Ety.

Radek: Tak skończyłem.

Radek: Okrąg jest styczny do osi układu współrzędnych w punktach A = (0,2) i B = (2,0) oraz jest styczny do prostej l w punkcie C = (1,a) , gdzie a > 1 . Wyznacz równanie prostej l .

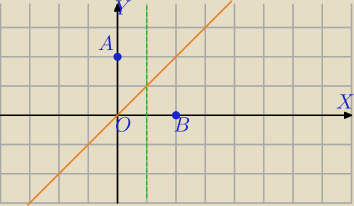
Mila: środek okręgu stycznego do osi leży na dwusiecznej kąta AOB, czyli prostej y=x ⇔ S(m,m) środek ma obie wsp. równe i równe R Poprowadź prostopadłą do OX w p. B i znajdziesz środek i R. Napisz

Radek: x=2

Mila: W takim razie: S=(2,2), R=2 teraz napisz równanie okręgu , potem znajdź punkt styczności C(1,a) należący do tego okręgu.

Radek: (x −2)²+(y−2)² = 4. Dalej już wiem. Dziękuję i dobranoc.

Mila: Dobranoc