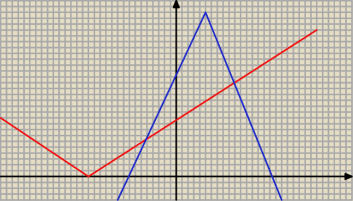
? Damo93: Zad.1..Zadania.info Dla jakich wartości parametru k równanie I x + 5 I + k² − 4k −26 = 0 ma dwa pierwiastki różnych znaków. Nie ogarniam tego zadania, za radom Piotr 10 − próbuje zrobić to graficznie ale nie bardzo wiem jak zapisałem coś takiego: f(x) = I x + 5 I = −k² + 4k + 26 rysuje te funkcje i nic mi to nie daje..

Damo93:

zawodus: źle

Damo93: to właśnie dlatego proszę o wyjaśnienie

zawodus: k − parametr.

ZKS: Zauważ że funkcja y = |x + 5| przecina oś OY w punkcie (0 ; 5) zatem różne rozwiązania będą dla −k² + 4k + 26 > 5.

Damo93: aha czyli że dla p > 5 są dwa rozwiązania innych znaków ?

zawodus: y=k − to funkcja stała y=k²+2k+1 − funkcja stała . . .

PW: Rysowanie nic nie da, funkcją jest |x+5|. Wyrażenie −k²+4k+26 to parametr (można powiedzieć, że jakaś liczba − na czas rozwiązania ustalona, dobrze by było oznaczyć to jednym symbolem, np. m − i wtedy rozstrzygać o liczbie rozwiązań, nawet rysując).

ZKS: Po lewej stronie osi OY masz rozwiązania ujemne po prawej stronie osi OY masz rozwiązania dodatnie.

Damo93: dobra już rozumiem dość nietypowe zadanko.. dzięki !

ZKS: Nietypowe? Przecież to standardowe zadanko.

Damo93: Mam również problem z zadaniem z wielomianem: Reszta z dzielenia wielomianu P(x) = 3x⁵ − 5x⁴ + ax³ + bx² + cx + d przez wielomian Q(x) = −3x⁴ + 2x³ + 8x² jest taka sama jak reszta z dzielenia Q(x) przez wielomian R(x) = 3x² −2x +1. Oblicz wartość współczynników a,b,c,d

ZKS: Gdzie jest problem?

ZKS: Wyznaczona reszta z dzielenia Q(x) przez R(x)?

Damo93: ale zazwyczaj jest inaczej zapisane, np. liczba rozwiązań funkcji w zależność od parametru k a tu ten parametr k jest −k2+4k+26 i to właśnie mnie zmyliło

zawodus: Standardowe rozwiązanie to 1. Podzielić Q(x) przez R(x)i zapisać resztę 2. Podzielić P(x) przez Q(x) i zapisać resztę Przyrównać i zobaczyć co będzie

Damo93:

	4
zacząłem ale nie dokończyłem, ja ten wielomian Q(x) zapisałem w postaci 3x2(x−2)(x +		) i
	3

te pierwiastki Q(x) chciał podstawić do P(x)

Damo93: zawodus podzieliłem i wyszło mi coś takiego : z dzielenia Q(x) / R(x) reszta = 6x + 3

	2		8
a z dzielenia P(x) / Q(x) reszta równa = (24		+ a)x3 + (		+ b)x2 + cx + d
	3		3

	8		2
jeżeli te reszty mają być równe to : d=3, c=6, b= −		i a = − 24		?
	3		3

Marcin: Co do pierwszego zadania. Dlaczego nie może być ≥5?

Damo93: właściwe to chyba może

Damo93: 0 a np. −3 są różne znaki,

Marcin: Ja właśnie dałem ≥5 i teraz już nie wiem sam czy zrobiłem dobrze czy źle

zawodus: To 0 jest jakiego znaku?

Marcin: żadnego

Damo93: Marcin: i jak ci wyszło ?

Marcin: <−3;7>, ale chyba jednak ma być (−3;7)