zadanie Magda: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=2522 proszę spojrzeć na moje wyliczenia ostatni komentarz czy mój sposób by przeszedł wynik rózni sie od wyniku Pana Jakuba ale robiłam innym sposobem proszę o zerknięcie do tematu i opinie Pozdrawiam

Magda: Widzę już bład źle wkleiłam w h1

Magda: tzn nie tak skróciłam ułamek i potem konsekwencje przeniosły się na wynik

Magda: Proszę jakąś mądrą osobe o wgląd

Magda: zielony oznaczam jako "b" niebieski jako h1 wpierw tw cosinusów: a²= 2b²−2b² *cos2α a²= 2b²(1− cos2α)

a2
	= b2
(2(1− cos2α))

	a2
b2=
	(2(1− cos2α))

	a
b=
	√2− 2cos2α

teraz obliczam x z tw pitagorasa a²=x² +b² x²=a² −b²

	a2(2− *2cos2α) −a2
x2=
	2− 2cos2α

	a2(2− *2cos2α −1 )
x2=
	2− 2cos2α

	a2(1− *2cos2α)
x2=
	2− 2cos2α

	a √(1− *2cos2α)
x=
	√2− 2cos2α

teraz porównuję trójkąty SJB i CBK bo są podobne kkk

h1		b
	=
a   2		x

2h1		a   b=   √2− 2cos2α
	=
a		a √(1− 2cos2α)   √2− 2cos2α

2h1		1
	=
a		√(1− 2cos2α)

	a
h1=
	2√(1− 2cos2α)

	a2
h12=
	4(1− 2cos2α)

teraz znowu korzystam z tw pitagorasa : i liczę trójkąt SYJ

	a√3		a2
H2 +		=
	6		4(1− *2cos2α)

	a2		a√3
H2=		−
	4(1− 2cos2α)		6

	6a2 −a√3(1− 2cos2α)
H2=
	24(1− 2cos2α)

	√6a2 −a√3− 2√3cos2α)
H=
	√24− 48cos2α)

V=1/3 Pp * H

	a2√3		√6a2 −a√3− 2√3cos2α)
V= 1/3 *		*
	4		√24− 48cos2α)

	a2√3√6a2 −a√3− 2√3cos2α)
V=
	12√24− 48cos2α)

	a2√18a2 −3ap− 6cos2α)
V=
	12√24− 48cos2α)

Magda: poprawiłam wszystkie obliczenia

Godzio: Błąd jeden dalej pozostał, ostatnie użycie twierdzenia Pitagorasa:

	1	a√3
H2 + (			)2 = h12
	3	2

Do reszty nie mam zastrzeżeń.

Magda: faktycznie ... normalnie jak się pisze długopisem trochę łatwiej ogarnąć a tutaj ciężko się pisze tymi skryptami czy Twoim zdaniem ten sposób może być ? wynik na pewno będzie sie różnił od wyniku Jakuba.

Magda: teraz znowu korzystam z tw pitagorasa : i liczę trójkąt SYJ

	a√3		a2
H2 +(		)2 =
	6		4(1− *2cos2α)

	a2		3a2
H2=		−
	4(1− 2cos2α)		36

	36a2 −3a2(1− 2cos2α)
H2=
	144(1− 2cos2α)

	a√36 −3+6cos2α)
H=
	12(1− 2cos2α)

V= Pp * H * 1/3

	a2√3		a√36 −3+6cos2α)
V=		* 1/3 *
	4		12(1− 2cos2α)

	a3√36√3 −3√3 +6√3cos2α)
V=
	144(1− 2cos2α)

poprawiłam według Twojej sugestii

Godzio: Sposób może być o ile wynik końcowy będzie poprawny. (nie musi być taki sam jak ten, który podał Jakub.

Magda: teraz znowu korzystam z tw pitagorasa : i liczę trójkąt SYJ

	a√3		a2
H2 +(		)2 =
	6		4(1− *2cos2α)

	a2		3a2
H2=		−
	4(1− 2cos2α)		36

	9a2 −3a2(1− 2cos2α)
H2=
	144(1− 2cos2α)

	a√9 −3+6cos2α)
H=
	12(1− 2cos2α)

V= Pp * H * 1/3

	a2√3		a√9 −3+6cos2α)
V=		* 1/3 *
	4		12(1− 2cos2α)

	a3√9√3 −3√3 +6√3cos2α)
V=
	144(1− 2cos2α)

poprawiłam według Twojej sugestii

Magda: ok dziękuję za informacje Pozdrawiam już poprawiłam wszystkie błedy jakie zobaczyłam. na kartce znacznie łatwiej sie to robi

Magda: teraz znowu korzystam z tw pitagorasa : i liczę trójkąt SYJ

	a√3		a2
H2 +(		)2 =
	6		4(1− *2cos2α)

	a2		3a2
H2=		−
	4(1− 2cos2α)		36

	36a2 −3a2(1− 2cos2α)
H2=
	6(1− 2cos2α)

	a√36 −3+6cos2α)
H=
	6(1− 2cos2α)

V= Pp * H * 1/3

	a2√3		a√36 −3+6cos2α)
V=		* 1/3 *
	4		6(1− 2cos2α)

	a3√36√3 −3√3 +6√3cos2α)
V=
	72(1− 2cos2α)

kolejna poprawka

Magda: wstawię całe zadanie może sie mój sposób komuś przyda

Magda: zielony oznaczam jako "b" niebieski jako h1 wpierw tw cosinusów: a²= 2b²−2b² *cos2α a²= 2b²(1− cos2α)

a2
	= b2
(2(1− cos2α))

	a2
b2=
	(2(1− cos2α))

	a
b=
	√2− 2cos2α

teraz obliczam x z tw pitagorasa a²=x² +b² x²=a² −b²

	a2(2− *2cos2α) −a2
x2=
	2− 2cos2α

	a2(2− *2cos2α −1 )
x2=
	2− 2cos2α

	a2(1− *2cos2α)
x2=
	2− 2cos2α

	a √(1− *2cos2α)
x=
	√2− 2cos2α

teraz porównuję trójkąty SJB i CBK bo są podobne kkk

h1		b
	=
a   2		x

2h1		a   b=   √2− 2cos2α
	=
a		a √(1− 2cos2α)   √2− 2cos2α

2h1		1
	=
a		√(1− 2cos2α)

	a
h1=
	2√(1− 2cos2α)

	a2
h12=
	4(1− 2cos2α)

teraz znowu korzystam z tw pitagorasa : i liczę trójkąt SYJ

	a√3		a2
H2 +(		)2 =
	6		4(1− *2cos2α)

	a2		3a2
H2=		−
	4(1− 2cos2α)		36

	9a2 −3a2(1− 2cos2α)
H2=
	36(1− 2cos2α)

	a√9−3+6cos2α)
H=
	6(1− 2cos2α)

V= Pp * H * 1/3

	a2√3		a√9−3+6cos2α)
V=		* 1/3 *
	4		6(1− 2cos2α)

	a3√9√3 −3√3 +6√3cos2α)
V=
	72(1− 2cos2α)

poprawiłam według Twojej sugestii

ZKS: Według Ciebie √3 * √6 = √6√3?

Magda:

	a3√18−18cos2α
V =
	72−144cos2α

bardzo źle się pisze tymi skryptami i się sama kilka razy pomyliłam. na kartce jest lepiej tak to było źle ZKS masz racje

Magda:

	a3√18+18cos2α
V=
	72−144cos2α

Godzio: No, to jeszcze dopracować ładnie wynik i nie jest najgorzej 18 + 18cos2α = 18(1 + cos2α) = 36cos²α

	a3cosα
V =
	12 − 24cos2α

Godzio: O ile α jest ostry, bo polecenia nie znam więc ciężko stwierdzić

Magda:

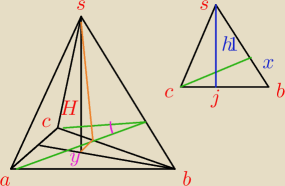
Magda: nooo Godzio teraz dałeś kolejne zagadnienie do zastanowienia się to jest to zadanie https://matematykaszkolna.pl/strona/2522.html