Metoda algeb. a metoda graf. meo: Uklad algebraiczny i graficzny Czy punkt przeciecia dwoch prostych, ktore zostaly rozawiazane metada algebraiczna i graficzna moze byc inny? Punkt przeciecia−metoda algeb.− (−3,2), metoda graf.−(3,−2). Oto uklad rownan x−y=−5 2x+y=−4

kochanus_niepospolitus: x = y−5 2x+y=−4 2y − 10 + y = −4 <=> 3y = 6 <=> y = 2 x = −3 błędnie narysowałeś proste

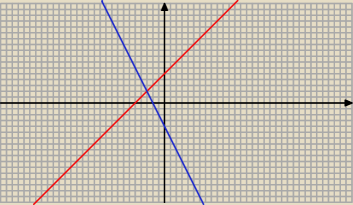
Janek191: x − y = − 5 2x + y = − 4 −−−−−−−−−−−−−− dodajemy stronami 3 x = − 9 / : 3 x = − 3 ===== y = x + 5 = − 3 + 5 = 2 P = ( − 3; 2) ================ Metoda graficzna: y = x + 5 y = − 2 x − 4 Rysujemy proste o podanych równaniach : ( czerwona i niebieska ) Odczytujemy P = ( − 3; 2) ====================== Jest ok

meo: ale jezeli naryuje proste wyznaczjac pkt z metody algeb. to miejsce ich przeciecia jest inne niz w metodzie graficznej

kochanus_niepospolitus: meo ... bo ŹLE rysujesz

kochanus_niepospolitus: I ja i Janek narysowaliśmy te proste ... masz tak je narysowane

meo: bo pkt przeciecia w obu metodach powinien byc taki sam, nie?