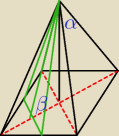
ostro sylwek: ostroslup prawidłowy czworokątny kąt przy wieszchołku ma miarę α, oblicz tangens kąta β jaki tworzy płaszczyzna przechodząca przez wieszchołek ostrosłupa i środki 2 sąsiednich boków podstawy

sylwek: mi wyszło że tgβ=2/tgα mógłby ktoś sprawdzić ?

dero2005: napisz jaki kąt przy wierzchołku: czy między wysokością a krawędzią boczną, czy między wysokością a ścianą boczną, czy inny?

sylwek: kąt ostry ściany bocznej przy wierzchołku ostrosłupa to α

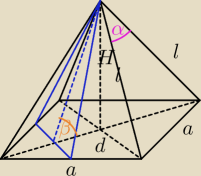dero2005: a² = 2l² − 2l²cosα a² = 2l²(1 − cosα)

	a2
2l2 =
	1−cosα

	a2
l2 =
	2(1−cosα)

d = a√2

d		a√2
	=
2		2

H² = l² − (^d₂)²

	a2		a2		a2		a2cosα
H2 = l2 −		=		−		=
	2		2(1−cosα)		2		2(1−cosα)

	a√cosα
H =
	√2√1−cosα

	H		a√cosα   √2√1−cosα
tgα =		=
	a√2   4		a√2   4

	cosα
tgα = 2√
	1−cosα