równanie sylwek: rozwiąż układ równań: x²=k²+36−6k

	30√7
k2=x2+36−		*x chodzi o wyliczenie k
	7

próbowalem to rozwiazywać ale nic mi z tego nie wychodzi. proszę o pomoc

pomocnik: Zauważ, że pierwsze równanie można zapisać x²−k²=36−6k a drugie

	30 √7
x2−k2=		*x−36.
	7

Stąd

	30 √7
36−6k=		*x−36.
	7

sylwek: ale wtedy są dwie niewiadome w jednym równaniu. da się to wyliczyć tak, żeby k było tylko liczbą ?

Bogdan:

	30
k2 = k2 + 36 − 6k + 36 −		x
	√7

	√7		7
x =		(12 − k) ⇒ x2 =		(144 − 24k + k2)
	5		25

7
	(144 − 24k + k2) = k2 + 36 − 6k ⇒ k2 + k − 6 = 0 ⇒ k = 2 lub k = −3
25

teraz trzeba podstawić k = 2 oraz k = −3 do obu zależności i sprawdzić poprawność obliczeń

Eta: Skąd masz taki układ równań? Napisz treść zadania

pomocnik:

	30		5
Możesz to zapisać w postaci 72−6k=		x /:6 ⇒ 12−k=		x /2
	√7		√7

	25		7
⇒(12−k)2=		x2⇒		(12−k)2=x2, a teraz podstaw np. do pierwszego równania i masz
	7		25

równanie kwadratowe.

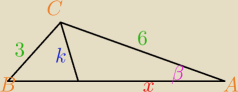sylwek: ETA w trójkacie ABC dane są kąt przy wierzchołku c równy 120, AC=6 BC=3 Dwusieczna kata ACB przecina bok AB w punkcie D oblicz dł CD Najpierw wyliczyłem sobie dł AB z tw cosinusów, potem cosinus β dalej znowu wstawiłem do tw cosinusów uwzględniając to co wyliczyłem i wyszedł uklad który podalem. Troche trudny sposób przyszedł mi do głowy. Da sie to jakoś krócej zrobić ?

sylwek: BOGDAN patrząc na tręść k=−3 odpada zostaje k=2 Dzięki za pomoc

sylwek: ?

sylwek: p

Bogdan:

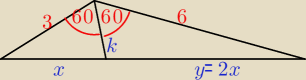
	3		6
z tw. o dwusiecznych w trójkącie		=		⇒ y = 2x
	x		y

z tw. cosinusów (x + 2x)² = 9 + 36 − 2*3*6*cos120^o ⇒ x = √7 z tw, cosinusów x² = 9 + k² − 2*3*k*cos60^o ⇒ k² − 3k + 2 = 0 i k > 0

sylwek: To rzeczywiście o wiele prościej. Dzieki wielkie

pomocnik: Skoro w tym temacie, to mając boki trójkąta a,b,c spróbujcie wyznaczyć długości tych części dwusiecznych, które są zawarte w trójkącie.

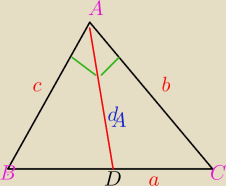
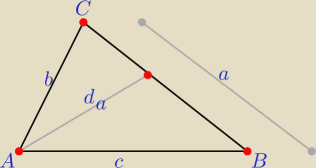Bogdan: a, b, c − długości boków trójkąta d_a − długość części dwusiecznej trójkąta zawartej w trójkącie i wychodzącej z A

	√ bc [(b + c)2 − a2]
da =
	b + c

Przyjemność wyprowadzenia tej zależności pozostawiam każdemu, kto ma na to chęć

5-latek: Witaj Bogdan

	2bc		A		2		A		p(p−a)
Lub da=		*cos		=		√b*c*p(p−a) gdzie cos		=√
	b+c		2		b+c		2		bc

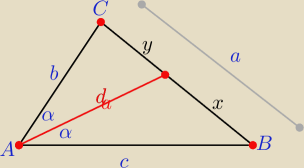Eta: No to się "pobawmy"

	b2+c2−a2
z tw. kosinusów : cos(2α)=		i cos(2α)=2cos2α−1
	2bc

to:

	b2+c2−a2+2bc		(b+c)2−a2
cos2α=		=
	4bc		4bc

	(b+c)2−a2
cosα=√
	4bc

	x		c		x2		c2
z tw. o dwusiecznej :		=		⇒		=
	y		b		y2		b2

z tw. kosinusów: x²=c²+d²−2dc*cosα i y²=b²+d²−2db*cosα

	c2+d2−2dccosα		c2
dzieląc stronami :		=
	b2+d2−2dbcosα		b2

po przekształceniach: b²d²−c²d²=2dbc*cosα(b−c) / : d d(b²−c²)=2bc*cosα(b−c) / : (b−c)

	2bc
d(b+c)=2bc*cosα ⇒d=		*cosα
	b+c

	2bc		(b+c)2−a2
d=		*√
	b+c		4bc

	√bc [(b+c)2−a2]
d=
	b+c

pomocnik: Że się Wam chciało "Rzuciłem" tak dla poćwiczenia w domowym zaciszu.

pomocnik: Skoro Eta tak ładnie przeprowadziła dowód, więc żeby było jeszcze bardziej elegancko należy dodać, że przejście z 4 do 5 linii (czyli spierwiastkowanie) wymaga zauważenia, że (b+c)²−a²>0; oczywiście łatwo to wynika ze wzoru skróconego mnożenia i nierówności między bokami trójkąta. Pozdr.

5-latek: No to ja moze tez sie pobawie (ale troche inaczej Niech d_A= AD bedzie dwusieczna kąta A

	dA		c
Z trojkata BAD mamy		=
	sinB		sin ADB

	A		pi−(B+C		π		B−C
ale kątADB=π −B−		= π−B−		=		−
	2		2		2		2

	c*sinB
Zatem dA=
	B−C   cos   2