planimetria może się uda bezendu: Przekątna trapezu równoramiennego dzieli jego kąt ostry na kąty o miarach α i β (α – kąt między przekątną i podstawą). Wyznacz stosunek pól trójkątów, na jakie przekątna ta podzieliła trapez.

	sin(2α+β)
K=
	sinβ

Mila: Wreszcie, zabrałeś się do roboty. Zaraz policzę.

bezendu: Cały czas liczę arkusze dzisiaj od 6 rano zrobiłem 10 arkuszy !

Marcin: A ja myślałem że ja za długo czasem siedzę

Eta: eeEtammm takie łatwe

Saizou : dokładnie takie łatwe, w sumie na jeden wzorek z tablic podstawić i gotowe xd

bezendu: Dla was łatwe, dla mnie problemowe...

bezendu: Was*

Saizou : podpowiem że każdy trapez równoramienny można wpisać o okrąg

Mila: Wynik dobry, to zadanie nie podoba mi się.( sformułowanie)

	a
Stosunek pól jest równy		, bo te Δ mają jednakową wysokość .
	b

bezendu: Podałem treść z arkusza. Nic nie zmieniałem.

Damo93: bezendu: skąd Ty bierzesz te arkusze ?

Mila: Wiem, to nie dla Ciebie uwaga.

bezendu: Dostałem prezent od Pani na święta i okres przed, ona sama układa ponad 50 arkuszy

Damo93: na jakim poziomie ? trudne czy typowe ?

Damo93: 10 arkuszy w ciągu dnia ! Ja max.3 jestem w stanie zrobić potem już nie myślę..

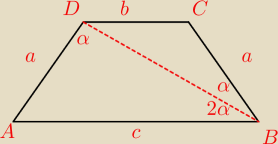
bezendu: Przekątna trapezu równoramiennego tworzy z dłuższą podstawą kąt 2α , a z ramieniem kąt α . Wykaż, że stosunek pól trójkątów, na które został podzielony trapez tą przekątną, jest równy

	sin5α
	sinα

	1
PΔABC=		absin3α
	2

Coś chyba nie tak

bezendu: I trudne i typowe. A czy mam jakiś wybór ? Muszę robić

Damo93: na zadania.info jest nawet generator arkuszy

bezendu: Ja nie szukam po internecie. Ale chyba nie jest w stanie wymyślić tyle zadań Ale dobry trop

Damo93: to właśnie wydawało mi się mało możliwe coby samemu ułożyć 50 arkuszy

bezendu: Mniejsza z tym skąd bierze, ja robię i mnie to nie interesuję. Mogą być nawet z kosmosu jak dla mnie

Eta:

bezendu: Jak dokończyć zadanie 21:42 ? Nie chcę żadnych linków !Spojrzę w link to tak jak bym się poddał, a wskazówka to coś innego !

Saizou : beznedu uważaj na słowa, bo zaraz kosmici przylecą i dadzą ci takie zadanie że nie będzie w stanie nawet go zrozumieć xd

Eta: I..... znów jesteś bardzo"miły"

Saizou : zawsze jestem bardzo miły, elokwentny i uprzejmy xd

Mila: Błąd w rysunku. ∡CDB=2α jako naprzemianległy. ∡ADB nie jest równy α ∡DAB=3α bo trapez równoramienny.

bezendu: Już wiem, źle to uzależniłem. Wszystko się poskracało pięknie ładnie

bezendu: kąt ADB=3α a kąt ADB=180−5α więc z sin(180−5α}=sin5α

Eta: Mój wpis był skierowany do bezendu .....

Saizou : no to fajnie xd

Saizou : haha aham....

Eta:

bezendu: Eta Wyraziłem swoje zdanie. Konstytucyjnie.

Mila: Coś pokręciłeś we wpisie 21:56.

bezendu: Kąt DAB=3α Kąt ADB 180−5α Po prostu trzeba brać te same boki aby się wszystko poskracało

bezendu: Mila masz jakieś zadanie na podobieństwo w trapezie równoramiennym ?

Mila: Szukam.

Mila: 1) W trapezie równoramiennym, którego podstawy mają długości a i b (a>b), a kąt ostry ma miarę α, połączono środki sąsiednich boków. Oblicz pole powstałego czorokąta. 2) Każdy z boków trójkąta o polu S podzielono na trzy części w stosunku !:10:1. oblicz pole sześciokata , którego wierzchołkami są punkty podziału boków.

Mila: 1:10:1 ma być, nacisnęłam omyłkowo silnię.

bezendu:

h		a−b   2
	=
sinα		cosα

	(a−b)sinα
h=
	2cosα

	a+b		(a−b)sinα
P=		*
	2		2cosα

	a2sinα−absinα+absinα−b2sinα
P=
	4cosα

	sinα(a2−b2)
P=
	4cosα

bezendu: 2. cecha podobieństwa bkb ?

bezendu:

	47S
2.
	48

1. Nie wiem co dalej z pierwszym ?

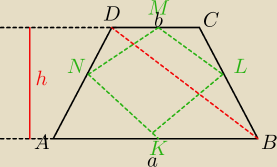
Mila: W (1) ΔAKN∼ΔABD, pole ABD potrafisz obliczyc , bo masz h i a. I tak z każdym "odciętym" trójkątem.

	a−b)*tgα
h=
	2

Przedostatnia linijka nie jest potrzebna, od razu mogłeś skorzystać z wzoru skróconego mnożenia, tam w liczniku masz przeciez mnożenie. (a+b)*(a−b)*sinα=(a²−b²)*sinα Nie rozumiem dlaczego tak masz rozpisane.

Mila: 2) błędny wynik.

Mila: Dobranoc Jutro spojrzę.

bezendu:

	48S
2.		?
	47

Dziś będę dopiero po 20 bo mam imprezę.

bezendu: ?

Mila: 1)

	(a−b)*tgα
h=
	2

	a+b
Ptrapezu=		*h
	2

	1
ΔAKN∼ΔABD w skali		( połączono środki boków)
	2

	1
PΔABD =		a*h
	2

	1		1		1
Pole ΔAKN jest 4 razy mniejsze⇔P ΔAKN =		*		a*h=		a*h
	4		2		8

Analogicznie :

	1
PΔKBL=		a*h
	8

	1		1
PΔLCM=		*PΔDCB=		*b*h=PΔMDN
	4		8

	a+b		1		1
PKLMN=		*h−(		a*h+		b*h) wykonaj działanie i podstaw za h
	2		4		4

Podaj wynik 2) za chwilę wskazówka

głupmen: zdaje mi się, że odwrotnie...

głupmen: to znaczy do drugiego

bezendu: Czemu z tg a nie tak ja policzyłem z sinusa ?

Mila: 2) dobry wynik 23:28: ( przepraszam, coś źle popatrzyłam na kartkę z rozwiązaniem)

141		47
	S=		S
144		48

bezendu: To mnie cieszy, że chociaż jedno zadanie zrobiłem ok.

głupmen: bezendu napisałeś źle 48/47,

głupmen: może walnąłeś się gdzieś w obliczeniach.... z fusów nie wróżę

głupmen: aha sorki, to Mila się pomyliła, na poprzednie posty nie zerkałem, ale tak 47/48 z 23:28 twój wynik bezendu był prawidłowy

bezendu: @głupem nie musisz mi nic potwierdzać, wystarczy jak zrobi to Mila

głupmen: gdybym nie zauważył błędu w rozumowaniu Mili, z kolei to człowiek renesansu, który się nie myli, to dalej byście brnęli i szukali rozwiązania

Marcin: Bezendu nieładnie tak. Ktoś chce CI pomóc, a Ty mu mówisz że sorry, ale nie Idę na siema

głupmen: też jestem człowiekiem i coś umiem, więc racz mi pozwolić sprawdzić twego nauczyciela

bezendu: Bo mówisz o fusach... Po co ? Wiem, że wynik wyszedł ok.

głupmen: nevermind miałem na myśli tego tg i sin i słowa tego się tyczyły

Mila:

sinα
	=tgα dla mnie to krócej, Twój wynik zgadza się z moim.
cosα

..Men, nie denerwuj się, dziękuję za sprostowanie. A pomyłki zdarzaja się wszystkim, z różnych przyczyn.

głupmen: ja jestem spokojny jak kwiat lotosu na tafli jeziora

Mila: Bezendu, też nie denerwuj się ,imprezę miałeś udaną? , mam dwa ładne trapeziki, załóż nowy wątek.

Mila: To może zadanie z kwiatem lotosu?

głupmen: pewnie ^^

bezendu: Tak, to były chrzciny. Impreza bardzo udana. Teraz ja wstawię w nowym wątku zadania problematyczne.

Mila: Nad powierzchnią jeziora wynurza się koniec łodygi lotosu, który wznosi się na pół łokcia nad wodą. Pod działaniem wiatru łodyga pochyla się i zanurza , aż wreszcie niknie pod wodą w odległości 2 łokciod miejsca w którym wyrosła.Oblicz młody matematyku, jak głęboka jest woda?

bezendu: Matematykiem chyba nigdy nie będę ale ty chyba z tw .pitagorasa ?

głupmen: ta

głupmen: hehe, fajne zadanie

Marcin: 1,5 łokcia?

bezendu: x²+2²=(x+0,5)² x²+4=x²+x+0,25 x=3,75 ? x−wysokość

głupmen: @Marcin mi wyszło 3²₄

Marcin: hehe Bo ja założyłem, ze ona ma 2 łokcie, bo na taką odległość opadła. Skoro miała dwa łokcie, i jak jeszcze stała, to miała 0.5 łokcia nad wodą, to 2−0,5=1,5 Ja tutaj nic nie liczyłem. Zabrałem się do tego niematematycznie, czyli źle

bezendu: ona wystawała na pół łokcia x+0,5

Marcin: Jeszcze nam się takie zadanko na maturze trafi Bezendu robiłeś dzisiejszą maturkę z zadania.info?

Mila:

	3
Bezendu , dobrze. 3		łokcia
	4

bezendu: Nie robiłem bo nie miałem czasu. Dziś po 01:00 zrobię.

głupmen: @Mila, aaa miałem na myśli 3/4 nie 2/4, źle mi się wpisało

Mila: Tak też pomyślałam.

Marcin: MIla chciałbym Ci się jakoś odwdzięczyć za to ze tutaj tak wszystkim pomagasz (jeszcze Ecie, czyli naszym dwóm nauczycielkom ), ale nie bardzo wiem jak to zrobić..

Mila: Dobre słowo wystarczy. Gdy zostaniesz milionerem,( w przyszłości) to przypomnij sobie o mnie.

Eta: Ooo tak! ... wtedy i o mnie też Pozdrawiam wszystkich

bezendu: Dobre słowo to zdecydowanie za mało za tą pracę....

Mila: Eto, liczymy, że to będzie w niedalekiej przyszłości.

Marcin: Pewnie że za mało Razem z chłopakami wyślemy wam jakiś podarunek (jeżeli dacie nam taką możliwość) O Tobie Eta przecież pamiętam

Marcin: Może ja już jestem milionerem?