indukcja matematyczna tyu: cześć, proszę o sprawdzenie zadania z indukcji matematycznej. wykaż że dla każdego n >2 , n∊N, zachodzi nierówność 3ⁿ⁺¹>4n+7. I krok − dla n=2 jest prawdziwa nierówność II krok − zakładam, że prawdą jest 3^k+1>4k+7, k≥2, k∊N III krok − na mocy założenia staram się dowieść prawdziwość 3^k+1+1>4(k+1)+7, k≥2, k∊N dowód: 3^k+1+1= 3^k+1 * 3 i na mocy założenia mam 3^k+1 * 3 >3 (4k+7) = 12k+21 12k+21>4(k+1)+7 12k+21>4k+4+7 8k>−10 8 * 2 = 16 i 16>−10 czy to co napisałem jest prawidłowe ? Proszę o sprawdzenie, bo jeśli jest to prawidłowe, to ruszam dalej z zadaniami, a nie mam kogo się spytać

tyu: proszę o sprawdzenie

pomocnik: No cóż dlaczego zaczynasz spr. od n=2?

pomocnik: Po drugie, nie ma II i III kroku. To co masz w II kroku, to założenie indukcyjne, a III krok to teza.

pomocnik: Poza tym po co Ci 8 * 2 = 16 i 16>−10?

tyu: pomyłka w zapisie, powinno być n≥2. Źle przepisałem z zeszytu

tyu: tak wiem, ze to założenie i teza − to był skrót myślowy,

tyu: w jednym rozwiązaniu zadania widziałem jak autor podstawiał na sam koniec za liczbę k pierwszą liczbę, dla której nierówność powinna być prawdziwa, dlatego podstawiałem tą k=2

pomocnik: Ok. Jeszcze mała poprawka do: 12k+21>4(k+1)+7 12k+21>4k+4+7 8k>−10

	10
k>−
	8

U Ciebie k≥2, więc jest to prawdą, tylko zawsze sprawdzaj, czy w odwrotną stronę Twoje rozumowania są prawidłowe, tzn. "od dołu do góry" w powyższym fragmencie.

pomocnik: tyu: w jednym rozwiązaniu zadania widziałem jak autor podstawiał na sam koniec za liczbę k pierwszą liczbę, dla której nierówność powinna być prawdziwa, dlatego podstawiałem tą k=2 Nie ma takiej potrzeby. Ważne żebyś napisał dlaczego tak jest.

tyu: czyli mam tutaj (8k>−10) na końcu ustalić k, czyli dzielę −10 przez 8, i patrzę czy tak wyliczone k jest większe/ równe 2. rozumiem. Dziękuję za sprawdzenie.

pomocnik: Nic nie ustalasz, tylko dzielisz, zastępujesz jedną nierówność inną równoważną.

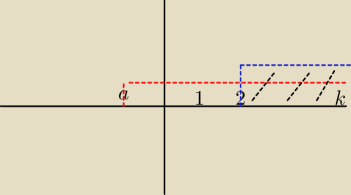
tyu: czyli w tym przypadku mogę sobie narysować wykres i zobaczyć, czy np jeden zakres pokrywa się z drugim

	−10
pkt a =
	8

pomocnik: Mniej więcej. Formalnie powinno wyglądać, to tak:

	−10
k≥2 ⇒k>		⇒8k>−10 ⇒ 12k+21>4k+4+7 ⇒ 12k+21>4(k+1)+7
	8

Albo przeprowadź dowód nie wprost.

tyu: dowód nie wprost to dla mnie zbyt trudne

pomocnik: E tam nie żartuj. Chcesz udowodnić, że 12k+21>4(k+1)+7 dla k≥2, więc zakładasz, że tak nie jest, tj.

	−10
istnieje naturalne k≥2, takie że 12k+21≤4(k+1)+7 ⇒ 12k+21≤4k+4+7⇒ 8k≤−10 ⇒ k≤		, a to
	8

jest sprzeczne z tym, że k≥2.

tyu: rozumiem, czyli to jest odwrócenie znaku > na ≤ i porównanie z założeniem k≥2, a czy można np zamienić znak > na <, czy koniecznie trzeba na ≤ ?

pomocnik: "przeciwieństwem" do > jest ≤. Więc musi być tak jak napisałem.

tyu: rozumiem, dziękuję za pomoc

pomocnik: Proszę