STEREOMETRIA
Pati: Cześć, mam problem z takim zadankiem:
Krawędź podstawy ostrosłupa prawidłowego trójkątnego ma długość a zaś krawędź boczna jest dwa
razy dłuższa. Oblicz pole przekroju tego ostrosłupa płaszczyzną, która przechodzi przez
krawędź podstawy i jest prostopadła do krawędzi bocznej.
Po prostu nie mam pojęcia jak narysować przekrój.
11 kwi 12:05
Draghan:
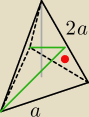
Ja bym to narysował w taki sposób

Czerwona kropka oznacza kąt prosty między płaszczyzną tego
przekroju, a krawędzią ściany.

11 kwi 12:12
Draghan: Chociaż nie. Płaszczyzna ma być prostopadła, a nie jej krawędź.
Zaraz wrzucę wersję 2.0

11 kwi 12:18
Pati: Okej, to czekam. Dzięki

11 kwi 12:27
Draghan:
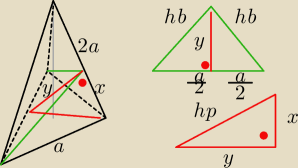
czerwona kropka − kąt prosty
hp − wysokość podstawy
hb − wysokość ściany bocznej
Jeśli nic nie pokręciłem, to tak może to wyglądać

11 kwi 12:29
Draghan: Rysunek trochę nieczytelny

W razie wątpliwości:
y jest wysokością przekroju
x jest fragmentem krawędzi bocznej, ale krawędź boczne nie ma długości x + 2a (tak − błędnie −
wynika z rysunku).
Coś jeszcze niejasne?

11 kwi 12:32
Pati: Okej super

Myślę, że teraz już sobie poradzę

11 kwi 12:33
Draghan: Ale głowy za ten rysunek nie daję

Żeby nie było − reklamacji nie uwzględniam

Miłego
liczenia

11 kwi 12:34
J: Rysunek 12 :12 jest własciwy dla zadania .
11 kwi 12:38
Draghan: W sensie, że krawędź tego przekroju ma być prostopadła do krawędzi ściany bocznej ostrosłupa

11 kwi 12:44
J: Dokładnie tak.
11 kwi 12:57
Draghan: Hm. Krawędź... Krawędź... Coś mi jednak nie daje spokoju.
A czy wysokość tego przekroju znajduje się wtedy również pod kątem prostym do krawędzi
ostrosłupa?
11 kwi 13:02
Draghan: Znaczy... Chodzi mi o tę wysokość przekroju, którą zaznaczyłem na drugim rysunku igrekiem.
11 kwi 13:04
J: Każda prosta należąca do płaszczyzny prostopadłej do krawędzi jest prostopadła do tej krawędzi
11 kwi 13:04
Draghan: Ech... Ale jestem

Dzięki

11 kwi 13:10
 Ja bym to narysował w taki sposób
Ja bym to narysował w taki sposób  Czerwona kropka oznacza kąt prosty między płaszczyzną tego
przekroju, a krawędzią ściany.
Czerwona kropka oznacza kąt prosty między płaszczyzną tego
przekroju, a krawędzią ściany.



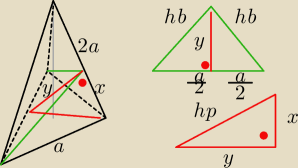 czerwona kropka − kąt prosty
hp − wysokość podstawy
hb − wysokość ściany bocznej
Jeśli nic nie pokręciłem, to tak może to wyglądać
czerwona kropka − kąt prosty
hp − wysokość podstawy
hb − wysokość ściany bocznej
Jeśli nic nie pokręciłem, to tak może to wyglądać 
 W razie wątpliwości:
y jest wysokością przekroju
x jest fragmentem krawędzi bocznej, ale krawędź boczne nie ma długości x + 2a (tak − błędnie −
wynika z rysunku).
Coś jeszcze niejasne?
W razie wątpliwości:
y jest wysokością przekroju
x jest fragmentem krawędzi bocznej, ale krawędź boczne nie ma długości x + 2a (tak − błędnie −
wynika z rysunku).
Coś jeszcze niejasne? 
 Myślę, że teraz już sobie poradzę
Myślę, że teraz już sobie poradzę 
 Żeby nie było − reklamacji nie uwzględniam
Żeby nie było − reklamacji nie uwzględniam  Miłego
liczenia
Miłego
liczenia 

 Dzięki
Dzięki 