punkt styczności Agusiakk95: punkt styczności okręgu o promieniu długości 4 cm wpisanego w trójkąt podzielił jeden z boków trójkąta na odcinki długości 6 i 8 cm. oblicz długości pozostałych boków trójkąta

Janek191: Błędne dane , bo 10² + 12² = 100 + 144 = 244 > 14² = 196

J: W zadaniu nie ma mowy,że trójkąt jest prostokątny...

Janek191: Faktycznie − nie zauważyłem Pozostałe boki tego trójkąta, mają długości: 13 cm i 15 cm.

Janek191: r = 4 a = 6 + 8 = 14 b = 8 + x c = 6 + x Obliczyć pole z wzoru P = 0,5 L*r i z wzoru Herona. Z porównania tych pól otrzymamy x , a następnie b i c.

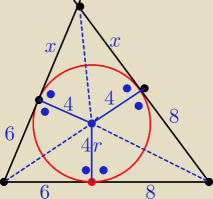
Janek191: Mamy L = 2*6 + 2*8 + 2x = 28 + 2x r = 4 więc P = 0,5 L*r = 0,5*( 28 + 2x)*4 = 56 + 4 x −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− p = 0,5 L = 14 + x p − a = ( 14 + x) − 14 = x p − b = ( 14 + x) − ( 8 +x) = 6 p − c = ( 14 + x) − ( 6 + x) = 8 P = √ (14 + x)*x*6*8 = √48 x*(14 + x) −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

Janek191: 56 + 4x = √ 48 x*( 14 + x) (56 + 4x)² = 48x*( 14 + x) 3 136 + 448 x + 16 x² = 672 x + 48 x² 32 x² + 224 x − 3 136 = 0 / : 32 x² + 7 x − 98 = 0 Δ = 49 − 4*1*( −98) = 441 √Δ = 21

	− 7 + 21
x =		= 7
	2

b = 8 + 7 = 15 c = 6 + 7 = 13 Odp. b = 15 cm. c = 13 cm ======================