oblicz pole Agusiakk95: oblicz pole figury ograniczonej osią OX oraz prostymi stycznymi poprowadzonymi przez punkt A(0,2) do okręgu o środku w punkcie S(−4,−5) i promieniu długości 3√5

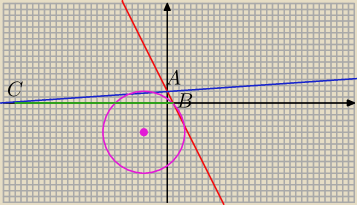
Janek191: A = ( 0 ; 2) Proste przechodzące przez punkt A mają równania postaci y = a x + 2 S = ( − 4; − 5 ) r = 3√5 Odległość tych prostych od punktu S jest równa d = r = 3√5 a x − y + 2 = 0 zatem

	I a*(−4) + (−1)*(−5) + 2 I
d =		= 3√5
	√a2 + 1

I − 4a + 7 I = 3√5*√a² + 1 − 4 a + 7 = 3 √5*√a² + 1 16 a² − 56 a + 49 = 45 a² + 45 29 a² + 56 a − 4 = 0 Δ = 3 136 − 4*29*(−4) = 3 600 √Δ = 60

	− 56 − 60
a =		= − 2
	58

lub

	− 56 + 60		2
a =		=
	58		29

Proste styczne do okręgu mają równania:

	2
y = −2 x + 2 oraz y =		x + 2
	29

=============================== Punkty przecięcia prostych z osią OX : y = − 2 x + 2 = 0 ⇔ x = 1 B = ( 1 ; 0 )

	2
y =		x + 2 = 0 ⇔ x = − 29 C = ( − 29; 0 )
	29

Pole Δ_ABC P = 0,5*I BC I *h = 0,5 *( 1 − ( −29))*2 = 30 ==================================