geometria Radek: Punkty A = (− 1,6) i B = (3,− 2) są wierzchołkami trójkąta ABC . Wiedząc, że punkt przecięcia się wysokości tego trójkąta ma współrzędne M = (0,− 1) oblicz współrzędne wierzchołka C . ?

Marcin:

Radek: wyznaczę tylko prostą prostopadłą (jedną) to nic nie da

Marcin: znasz współrzędne dwóch punktów, możesz z tego wyznaczyć drugą wysokość. Ma przechodzić przez punkt B i M

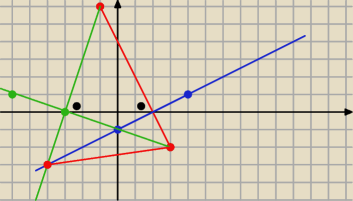
Mila: 1)Niebieska prosta jest prostopala do AB i przechodzi przez p. M− napisz jej równanie. 2) Napisz prostą przechodzącą przez A i M ( zawiera drugą wysokość)− 3) Napisz równanie prostopadłej do AM i przechodzącej przez B. 4) Punkt przecięcia niebieskiej prostej i ostatniej prostej to będzie punkt C

Radek: Dziękuję Pani, z tego wyszło bardzo ładnie.

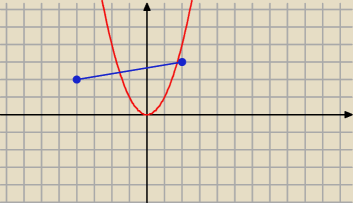
Radek: Dane są punkty A = (1,3),B = (−4 ,−2 ) . Wyznacz taki punkt C = (x ,y) , gdzie x ∈ (−1 ,2) leżący na paraboli o równaniu y=x² , aby pole trójkąta ABC było największe. jak znaleźć C ? (x,x²) ? P=0,5|..| z tego wzoru ?

Marcin: Chodzi Ci o ten wzór?

	1
P=		|(xb−xa)(yc−ya)−(yb−ya)(xc−xa)|
	2

Też bym z tego skorzystał

Marcin: Na szczęście ten wzór jest w tablicach, bo za nic bym go nie zapamiętał

Radek: Ok.

Radek: Wyszło z tego. dziękuję po raz kolejny.

Marcin: Oby na maturze tak nam szło

Radek: Tobie, dobrze idzie, ja muszę jeszcze pytać. Może przez to 28 dni coś się poprawię

Marcin: Każdy ma swoje słabe strony. Ja leżę z prawdopodobieństwa.Poprawisz poprawisz

zawodus: Da się go zapamiętać, ale w wersji z wyznacznikiem

Radek: Jednak ta odpowiedź jest nie poprawna, chyba zły ten sposób odnośnie 23:04

Marcin: C=(−4;−3), to zła odpowiedź?

Radek: Mi wychodzi −3,−2

Marcin: Na rysunku z 23:19 masz ładnie zaznaczone. Jak chcesz to mogę Ci podać obliczenia. Może gdzieś się po prostu machnąłeś w obliczeniach?

Radek: to poproszę.

Marcin: B=(3,−2) a M=(0,−1) Prosta przechodząca przez tez dwa punkty to: −2=3a−1 −1=3a ()/3

	1
a=−
	3

	1
Prosta ma równanie y=−		a−1
	3

Szukasz teraz do niej prostopadłej, więc ma ona współczynnik przy a=3, a że ma przechodzić przez A, to jej równanie to: y=ax+b A = (− 1,6) 6=−3+b b=9 y=3a+9 Teraz szukasz tylko punktu przecięcia się dwóch prostych Niebieska ma równanie:

	1
y=		x−1, a zielona y=3a+9
	2

Masz układ równań który już raczej rozwiążesz.

Radek: Jaki układ. Ja robiłem tak jak podała Pani Mila.

Marcin: No ale mając dwie proste jak policzysz ich punkt przecięcia, co?

	1
y=		x−1
	2

y=3x+9 <− wcześniej omyłkowo miałem tutaj a, wybacz.

1
	x−1=3x+9 *()2
2

x−2=6x+18 −5x=20 x=−4

Mila: Marcin, Radek , dałam zadania dla Bezendu, też popatrzcie.

Radek: Dziękuję ja teraz z bryłami walczę.

Marcin: Dziękuję bardzo. Czasem staram się robić zadania dla bezendu, ale wolę się nie wtrącać, bo nie chce go denerwować Ogólnie to przeważnie i tak jadę arkusze

Mila: Rób dla siebie.

Radek: i mam pytanie https://matematykaszkolna.pl/strona/3405.html skąd wiadomo które boki są takie same w tym trójkącie ?

Marcin: Miloo a myślisz że lepiej dla mnie będzie jak będę sobie sam rozwiązywać arkusze, czy może lepiej będzie jak będę tutaj szukać zadań?

Piotr 10: to wynika z nierownosci trójkata suma dwoch bokow jest wieksza od trzeciego ( pomysl nad tym )

Piotr 10: Jesli przyjmiemy, że trojkat jest rownoramienny o ramionach 22 to mamy 22+22 > 61 i otrzymujemy sprzecznosc a zatem bok musi miec 61

Marcin: Chodzi Ci o to skąd wiemy, że akurat tak będzie ustawiony ten trójkąt równoramienny? Wszystko zależy od rysunku. Tam masz najpierw obliczone boki tego trójkąta w podstawie, a później dopiero zauważenie że akurat tak ma on wyglądać.

Marcin: Aa o to chodziło

Piotr 10: Dziwne, ze tego nie ma w rozwiazaniu. Bo jakby ta nierownosc byla spelniona, to wtedy by byly II przypadki

Mila: Marcinie rozwiązuj zadania z arkuszy, tam masz przegląd materiału, tutaj są zadania, które komuś sprawiają trudności, sa wśród nich banalne, ale są też trudniejsze i ciekawe. Radku, tam masz obliczenia, z kórych wynika jakie są długości boków

Marcin: Autorowi wydawało się to zbyt oczywiste

Marcin: Dobrze, dziękuję

Radek: Dzięki