Na ile sposobów da się ułożyć:
ZosiaZamoyska: Na ile sposobów da się ułożyć 4 cyfrowe liczby, których suma da 7, zakładając że każda cyfra w
liczbie jest większa od 1? Wzór, generalnie potrzebny

10 kwi 21:42
PW: Zosiu, o co Ty pytasz? Przeczytaj jeszcze raz co napisałaś
10 kwi 21:45
Ajtek:
Na co ten wzór

Na sumę czterech cyfr większych od jedynki, których suma wynosi 7

10 kwi 21:45
Ajtek:
Witaj
PW 
.
10 kwi 21:46
ZosiaZamoyska: *Na ile sposobów da się ułożyć 4 cyfrowe liczby, których suma cyfr da 7

10 kwi 21:59
zawodus: wg mnie 4*2=8

10 kwi 22:01
ZosiaZamoyska: czemu razy 2?
10 kwi 22:02
52: zawodus nie za szybko ?
10 kwi 22:02
zawodus: 52 uwierz długo nad tym myślałem

10 kwi 22:06
52:
4 1 1 1 − suma cyfr 7
3 2 1 1 − suma cyfr 7
4+4*3=16 a tak ?
10 kwi 22:08
52: jeszcze jest
2 2 2 1 − suma cyfr 7
to razem powinno być 4+4+4*3=20
10 kwi 22:09
zawodus: To mogą być te "jedynki" czy nie?
10 kwi 22:09
52: A jak to zrobiłeś bez ''jedynek'' ?
10 kwi 22:10
PW: Zosiu, to mają być 4−cyfrowe (czterocyfrowe) liczby? Tak to się pisze − z myślniczkiem albo
słownie. Napis "4 cyfrowe liczby" jest bez sensu, oznacza jakieś cztery "cyfrowe liczby".
Dalej piszesz "których suma da 7". Suma tych liczb ma dać 7, czy suma cyfr każdej z liczb
ma być równa 7?
I myślę, że nie "ułożyć", ale "utworzyć".
N i e p i s z z a d a ń "z głowy", cytuj dosłownie.
10 kwi 22:10
zawodus: No właśnie napisałem, że 4*2=8

10 kwi 22:10
PW: Przecież w treści zadania jest powiedziane: "każda cyfra w liczbie jest większa od 1".
10 kwi 22:12
Draghan: A to się da w ogóle utworzyć taką choćby jedną liczbę?

10 kwi 22:13
52: A mógłbym zobaczyć te możliwości, bo całkowicie się pogubiłem
10 kwi 22:13
ZosiaZamoyska: a czemu tak, 52 ? A jak by to było, gdyby zamiast 4 było 2, a zamiast 7 byłoby 6? (z pewnych
źródeł wiem, że dobrze wyszło 20)
10 kwi 22:19
PW: Proszę bardzo: 4−cyfrowa liczba o sumie cyfr równej 7
222 (trzy najmniejsze z możliwych według treści zadania i nie ma rady − czwarta musiałaby być
1.
Draghan ma rację

albo nie rozumiemy treści zadania.
10 kwi 22:19
zawodus: To jest nas trzech

10 kwi 22:20
ZosiaZamoyska: PRZEPRASZAM! WIĘKSZA RÓWNA JEDEN!
10 kwi 22:21
52: Zosia no jest tyle możliwości
2 2 2 1 − 4 sposoby
3 2 1 1 − 4*3 sposoby
4 1 1 1 − 4 sposoby
4+4*3+4=20
10 kwi 22:22
PW: Aha, i każda cyfra w liczbie jest większa od 1. Ja mam inne wyobrażenie "większości".
10 kwi 22:26
Draghan: PW, to zwykła pomyłka

Każdemu się może zdarzyć

(a ja coś o tym wiem


)
10 kwi 22:28
Mila:
Tych liczb można utworzyć, tyle ile jest rozwiązań równania :
x
1+x
2+x
3+x
4=7, gdzie x
i∊N
+⇔
10 kwi 22:30
ZosiaZamoyska: Dlaczego 6? Dlaaczego 3? Oo Ogarniam, że symbol Newtonowski i kombinatoryka, wariacje z
powtórzeniami...
10 kwi 22:32
Mila:
Zosiu , jesteś w LO, czy na studiach?
10 kwi 22:33
ZosiaZamoyska: W 1 gimnazjum, a co?
10 kwi 22:35
Mila:
To spróbuj zrozumieć sposób 52.
10 kwi 22:36
zawodus: Mila Chciała cię nauczyć sposobu z matematyki dyskretnej

wzór
n{n+k−1}{k−1}

10 kwi 22:38
PW:
Znaczy się rozwiązałaś zadanie o 4 jednocyfrowych większych od zera liczbach, których suma daje
7. Brawo dla Zosi
10 kwi 22:38
10 kwi 22:38
ZosiaZamoyska: Znam matematykę dyskretna, tylko nie wiedziałam, jak to ogarnąć do końca... Generalnie treść
zadania brzmi: "W Bajtocjii odbywają się wybory prezydenckie. Wiadomo, że jest K kandydatów na
fotel prezydenta, oraz N mieszkańców uprawnionych do głosowania. Oczywiście każdy kandydat
głosuje na siebie, zatem przyjmijmy, że ma przynajmniej jeden głos. Ile może być różnych
wyników głosowania?" Ale skróciłam go do tej wersji, którą podałam. Bardziej ogarniam sposób
Mili niż 52

10 kwi 22:43
ZosiaZamoyska: A wszystko potrzebne mi do zadania z informatyki

10 kwi 22:45
zawodus: 52 po prostu rozpisał wszystkie możliwości

10 kwi 22:46
ZosiaZamoyska: Spoko, dzięki wszystkim

10 kwi 22:48
PW: Zosiu, za każdym razem przedstawiasz swoistą interpretację zadania zamiast dokładnej treści.
Szkoda czasu. Przepraszam, więcej nie będę.
10 kwi 22:55
ZosiaZamoyska: 
Po prostu myślałam od tym od pewnego czasu, i to był wniosek, do jakiego doszłam "skrócenie
tego zadania w jednym zdaniu"....
10 kwi 23:05
Mila:
Zosiu, w matematyce nie ma pośpiechu. Najlepiej treść zadania podawać bez skrótów
, a rozwiązania jak najprostsze.
10 kwi 23:10
Mila:
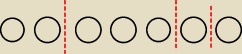
Rozwiązanie równania z 22:30 obrazowo można przedstawić tak.
Masz 7 kul i chcesz je rozłożyć do 4 szuflad, tak, aby żadna nie była pusta.Wstawiasz 3
przegrody.
Na rysunku masz sytuację:
2+3+1+1=7 kule rozłożone , to jeden ze sposobów.
Jednak dla tych przegród możesz wybrać inne 3 miejsca z 6 możliwych.
To wyrażamy wzorem:
10 kwi 23:18
ZosiaZamoyska: Tak tak, widzę i rozumiem

Symbol Newtonowski znam nie od dziś

10 kwi 23:28

 Na sumę czterech cyfr większych od jedynki, których suma wynosi 7
Na sumę czterech cyfr większych od jedynki, których suma wynosi 7
 .
.





 albo nie rozumiemy treści zadania.
albo nie rozumiemy treści zadania.

 Każdemu się może zdarzyć
Każdemu się może zdarzyć  (a ja coś o tym wiem
(a ja coś o tym wiem 
 )
)
 wzór
n{n+k−1}{k−1}
wzór
n{n+k−1}{k−1}






 Po prostu myślałam od tym od pewnego czasu, i to był wniosek, do jakiego doszłam "skrócenie
tego zadania w jednym zdaniu"....
Po prostu myślałam od tym od pewnego czasu, i to był wniosek, do jakiego doszłam "skrócenie
tego zadania w jednym zdaniu"....
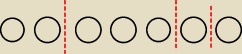 Rozwiązanie równania z 22:30 obrazowo można przedstawić tak.
Masz 7 kul i chcesz je rozłożyć do 4 szuflad, tak, aby żadna nie była pusta.Wstawiasz 3
przegrody.
Na rysunku masz sytuację:
2+3+1+1=7 kule rozłożone , to jeden ze sposobów.
Jednak dla tych przegród możesz wybrać inne 3 miejsca z 6 możliwych.
To wyrażamy wzorem:
Rozwiązanie równania z 22:30 obrazowo można przedstawić tak.
Masz 7 kul i chcesz je rozłożyć do 4 szuflad, tak, aby żadna nie była pusta.Wstawiasz 3
przegrody.
Na rysunku masz sytuację:
2+3+1+1=7 kule rozłożone , to jeden ze sposobów.
Jednak dla tych przegród możesz wybrać inne 3 miejsca z 6 możliwych.
To wyrażamy wzorem:
 Symbol Newtonowski znam nie od dziś
Symbol Newtonowski znam nie od dziś 