geometria
Radek:
Okrąg wpisany w trójkąt ABC ma równanie x2−8x+y2 + 2y = 3 . Oblicz tg ∡BAC jeżeli A = (−
4,− 7) .
Mam równanie (x−4)2+(y−1)2=20
jak wyznaczyć pozostałe punty
10 kwi 21:15
zawodus: Co jeszcze wiemy o trójkącie ABC?
10 kwi 21:16
Radek:
Nic
10 kwi 21:21
zawodus: trójkąt jest prostokątny tak?
10 kwi 21:22
Radek:
Skąd to wiesz ?
10 kwi 21:27
zawodus: Dobra, źle spojrzałem na ten kąt

Trójkątów spełniających dane z zadania jest nieskończenie wiele. − nie wyznaczysz Punktów B i C

1. Sporządź rysunek pomocniczy, a zobaczysz co trzeba zrobić.
10 kwi 21:33
Radek:
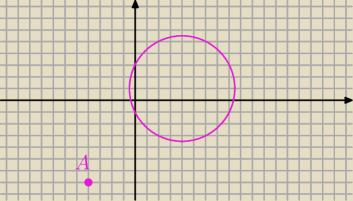
10 kwi 21:35
zawodus: Ok to teraz szukasz stycznych do okręgu z punktu A

10 kwi 21:36
Radek:
Czemu styczne ?
10 kwi 21:36
zawodus: masz mieć okrąg wpisany tak? czyli okrąg musi być styczny boków trójkąta

10 kwi 21:39
Mila:
Połącz punkt A ze środkiem okręgu, naszkicuj styczną i promień do punktu styczności.
Możesz obliczyc :
sinus i cosinus połowy szukanego kąta.....
10 kwi 21:40
Damo93:
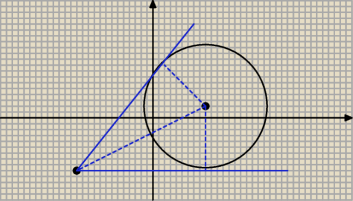
promień masz, liczysz długość AS potem z twierdzenia przeciwprostokątną..
10 kwi 21:41
Radek:
Ale co dadzą mi te styczne? Będę miał 2 punkty i skąd wiadomo, że to punkt B i C
y=2x+1
Mam te styczne
10 kwi 21:42
zawodus: lub od razu tg kąta przecięcia dwóch prostych

10 kwi 21:43
zawodus: To nie będą B i C. Okrąg ma być wpisany w trójkąt...
10 kwi 21:43
Radek:
no skro to nie będą B i C to co to za punkty ?
10 kwi 21:53
Damo93: nie musisz liczyć pozostałych punktów bo to z tą ilością danych jest nawet nie możliwe, oblicz
SA promień masz dany, liczysz przeciwprostokątną i masz połowę tg

10 kwi 21:53
Damo93:
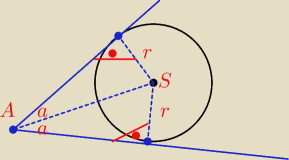
//
10 kwi 21:57
Radek:
Nadale tego nie rozumie, rysunek mam.
10 kwi 22:01
zawodus: masz mieć tg kąta2α

policz tg kąta α z rysunku
DAmo93 
10 kwi 22:03
zawodus: Ja jestem jednak za tym, żeby kąt policzyć ze wzoru:
10 kwi 22:04
Radek:
Ok policzę z tego wzoru z tablic który podałeś
10 kwi 22:07
zawodus: Bo wymaga to tylko znajomości równań prostych

10 kwi 22:08
10 kwi 22:08
zawodus: ok
można też było bez wyznaczania stycznych tylko z trójkątów prostokątnych policzyć sin2α i cos2α
i potem tg2α

10 kwi 22:13
Radek:
Jednak prostsze to co podałeś. Dziękuję !
10 kwi 22:18
 Trójkątów spełniających dane z zadania jest nieskończenie wiele. − nie wyznaczysz Punktów B i C
Trójkątów spełniających dane z zadania jest nieskończenie wiele. − nie wyznaczysz Punktów B i C
 1. Sporządź rysunek pomocniczy, a zobaczysz co trzeba zrobić.
1. Sporządź rysunek pomocniczy, a zobaczysz co trzeba zrobić.



 promień masz, liczysz długość AS potem z twierdzenia przeciwprostokątną..
promień masz, liczysz długość AS potem z twierdzenia przeciwprostokątną..


 //
//
 policz tg kąta α z rysunku DAmo93
policz tg kąta α z rysunku DAmo93 

