Graniastosłup
Arni: Objętość graniastosłupa prawidłowego czworokątnego jest równa 16 a pole powierzchni bocznej
jest równe 32 Oblicz cosinus kąta utworzonego przez przekątne ścian bocznych wychodzące z tego
samego wierzchołka graniastosłupa.Proszę o pomoc
10 kwi 20:26
Janek191:
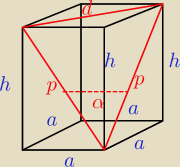
Mamy
V = a
2 *h = 16
P
b = 4a*h = 32 ; dzielę stronami
a = 2
====
4*2*h = 32 ⇒ 8 h = 32 ⇒ h = 4
h = 4
====
p
2 = a
2 + h
2 = 2
2 + 4
2 = 4 + 16 = 20 = 4*5
p =
√4*5 = 2
√5
==============
d = a
√2 = 2
√2
=============
Z tw. Kosinusów mamy
( 2
√2)
2 = (2
√5)
2 + (2p{5])
2 − 2* 2
√5*2p{5]*cos α
8 = 20 + 20 − 8*5*cos α
8 = 40 − 40 cos α
40 cos α = 32
| | 32 | | 4 | |
cos α = |
| = |
| = 0,8 |
| | 40 | | 5 | |
α ≈ 36
o 50'
===========
10 kwi 20:49
Janek191:
Mamy
V = a
2 *h = 16
P
b = 4a*h = 32 ; dzielę stronami
a = 2
====
4*2*h = 32 ⇒ 8 h = 32 ⇒ h = 4
h = 4
====
p
2 = a
2 + h
2 = 2
2 + 4
2 = 4 + 16 = 20 = 4*5
p =
√4*5 = 2
√5
==============
d = a
√2 = 2
√2
=============
Z tw. Kosinusów mamy
( 2
√2)
2 = (2
√5)
2 + (2p{5])
2 − 2* 2
√5*2p{5]*cos α
8 = 20 + 20 − 8*5*cos α
8 = 40 − 40 cos α
40 cos α = 32
| | 32 | | 4 | |
cos α = |
| = |
| = 0,8 |
| | 40 | | 5 | |
α ≈ 36
o 50'
===========
10 kwi 20:51
Arni: dziękuję Janek w międzyczasie nadal próbowałem zrobić to zadanie i wszystko szło zgodnie z
planem Jeszcze raz dzięki
10 kwi 20:53