help lola d: Prosze o pomoc, Zbadaj monotoniczność ciągu an, określonego wzorem: a) a_n = n² − 4n − 5

	1
b) an = 4 +
	n

	3n+5
c) an = −
	n+1

Tadeusz: licz a_n+1−a_n

	an+1
lub
	an

lola d: a w a) jaka to funkcja skoro r nie jest stałe tylko wychodzi 2n−3?

Tadeusz: ... tyle, że Ciebie nie pytają o to jaki to ciąg ... pytają o monotoniczność − (Skoro a_n+1−a_n jest zależne od n ... to arytmetyczny on nie jest) −

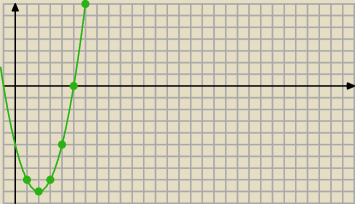
Tadeusz: ... a trzecia metoda jest taka Skoro a_n=n²−4n−5 ... to kolejne wyrazy leżą na krzywej, która znasz −

xpp: no tak, to wiem ale co wtedy z tą monotonicznością, no bo jak r lub q jest dodatnie to a_n rośnie, a jak ujemne to an malejący. mi wyszło w a) r = 2n −3, to będzie a_n niemonotoniczny?

Tadeusz: 1) nie nazywaj tego r ... bonie jest to ciąg arytmetyczny. Jest to różnica między kolejnymi wyrazami ale nie r. Musisz przeanalizować gdzie ona jest dodatnia (ciąg rośnie) a gdzie ujemna (ciąg maleje)