Planimetria Marcinek: W trójkącie ABC dane są długości boków: AB = 4 , AC = 6 , BC = 8 . Oblicz długości odcinków, na jakie dzieli bok BC wysokość opuszczona z wierzchołka A . Może mi ktoś wyjaśnić dlaczego nie chce to wyjść w następujący sposób ? Licze pole trójkąta ze wzoru na połowę obwodu i wszystkie boki , następnie wyliczam H opuszczone na bok BC i potem próbuje z pitagorasa na trójkąt BKA tyle, że KB wychodzi ujemne .. Co jest złego w tym sposobie ?

Tomasz: hmm ciężka sprawa

Marcinek : pomoże ktoś ?

Mila:

	6+4+8
p=		=9
	2

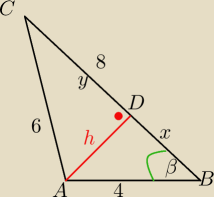
P_Δ=√9*(9−4)*(9−6)*(9−8)=√9*5*3*1=3√15

	1
3√15=		*8*h
	2

3√15=4h

	3√15
h=
	4

W ΔADB: x²+h²=4²

	3√15
x2+(		)2=16
	4

	9*15
x2+		=16
	16

	7		9
x2=16−8		=7
	16		16

	121
x2=
	16

	11		3
x=		=2
	4		4

	3		1
y=8−2		=5
	4		4

II sposób Oblicz cosβ z tw. cosinusów