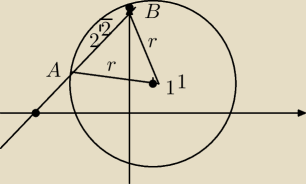
ok Radek: Napisz równanie okręgu o środku S(1,1) , który na prostej o równaniu x − y + 4 = 0 odcina cięciwę AB długości 2√2 . Wykonaj rysunek Proszę o pomoc. Bezradny jestem w tym zadaniu

ja:

Radek: Ale jak wyznaczyć r ? Jaki to trójkąt ?

Piotr 10: trojkat rownoramienny

bezendu: odległość punktu od prostej to h potem z Tw.pitagorsa policzysz promień r=√10

Domel: Obróciłem troszkę rysunek, żebyś miał łatwiejszy pogląd a = 2√2

	α
β = 90° −
	2

No i spróbuj z twierdzeń sinusów, cosinusów i wylicz r − dalej to już skorzystanie z ogólnego wzoru na równanie okręgu

Radek: Dziękuję Domelku Już zrobione !

Radek: Znajdź równanie prostej, zawierającą dwusieczną tego kąta, utworzonego przez proste k : x + 3y − 1 = 0 oraz l : 6x − 2y+ 1 = 0 , do obszaru którego należy punkt P (3,1) . Wiem jak wyznaczyć równania dwusiecznych i tylko tyle ?

Piotr 10: no jak teraz wyszły Ci dwa rownania prostej to teraz musisz wybrac jedna z nich do ktorej nalezy punkt P

Radek: Ale tu chodzi o obszar ? !

Rafał28: Narysuj sobie prostą k i prostą l i zaznacz punkt P. Punkt P będzie w jednej z ćwiartek na które te proste dzielą się i tam właśnie, gdzie będzie punkt P masz wyznaczyć równanie dwusiecznej. Tzn w tym obszarze co jest punkt P. Mam nadzieję, że rozumiesz A i żeby była jasność Punkt P nie musi należeć ani do prostych k, l ani do dwusiecznych.

Radek: −11x+10y−3=0 13x−y+1=0 10y=11x+3

	11		3
y=		x+
	10		10

13x−y+1=0 −y=−13x−1 y=13x+1

Radek: ?

Radek: ?

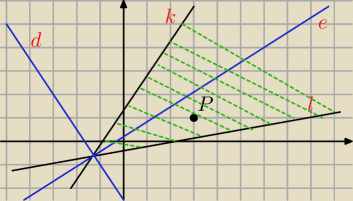
Rafał28: To są rozumiem twoje dwusieczne? Chodziło mi o proste k i l. Patrz Rysunek. Punkt P leży w pewnym obszarze (zakreskowany na zielono), czyli chodzi w zadaniu o dwusieczną e bo też tam leży w tym obszarze. To jest rysunek pomocniczy.

Radek: Ok rozumie, dziękuję i dobranoc.

Rafał28: Dobranoc.