Ostrosłupy
Oskar: Krawędź podstawy ostrosłupa prawidłowego szcześciokątnego ma długość a. Ściana boczna tworzy z
podstawą kąt 60stopni. Oblicz objętość tego ostrosłupa oraz sinus kąta krawędzią boczną a
krawędzią podstawy tego ostrosłupa.
Jest ktoś w stanie pomóc mi z tym? Z góry dziękuję

9 kwi 19:53
Rafał28:
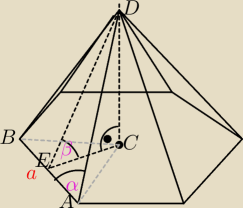
β = 60
o
Podstawa ostrosłupa to sześć przystających trójkątów równobocznych.
Popatrz na ΔACB, ΔCDE, ΔAED wiedząc, że
ΔACB równoboczny
E środek AB
DE wysokość ściany bocznej
sin α = ?, szukana wartość w zadaniu
9 kwi 20:52
dero2005:
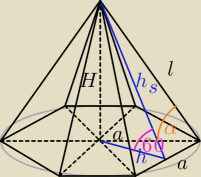
h
s = a
√3
l =
√hs2 + (a2)2 =
9 kwi 22:46
Rafał28:
dero dobrze kąt α?

9 kwi 22:56
Bogdan: V=1/3*Pp*CD −Objętość ostrosłupa −−−> jedna trzecia pola podstawy razy wysokość
trójkąt ACB jest równoboczny
Pp=6*(a2*√3/4) − pole podstawy jest sumą 6−ciu pól trójkąta o boku "a"
Pp=a2*3/2*√3
Z trójkąta ABC EC=a* √3/2 jest to wysokość w trójkącie równobocznym
Z trójkąta ECD ( połowa trójkąta równobocznego o boku 2*EC)
ED=2*EC=a*√3
DC=√ED*√3 / 2 ⇒ DC=3/2 * a
AD=√(a/2)2+ED2 ⇒ AD=a/2 *√13
po podstawieniu
V=1/3*(a2*3/2*√3*3/2*a2*√3) = 9/4*a3
sin(α)=ED/AD= itd
9 kwi 23:51
dero2005:
źle zaznaczyłem kąt α bo pobieżnie przeczytałem treść zadania
10 kwi 08:12
Bogdan:
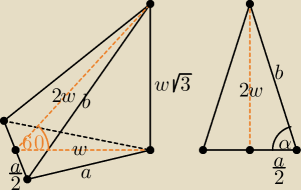
Włączam swój wpis, aby skorygować błędy w zapisach mojego imiennika (np. a
2*a
2 = a
3)
| | 1 | | 1 | | 1 | | 1 | |
Objętość V = |
| *6* |
| a2√3*w√3 = |
| a2√3* |
| a√3*√3 = ... |
| | 3 | | 4 | | 2 | | 2 | |
| | a | | 2w | |
b2 = 4w2 + ( |
| )2 = ..., sinα = |
| = ... |
| | 2 | | b | |
10 kwi 12:40

 β = 60o
Podstawa ostrosłupa to sześć przystających trójkątów równobocznych.
Popatrz na ΔACB, ΔCDE, ΔAED wiedząc, że
ΔACB równoboczny
E środek AB
DE wysokość ściany bocznej
sin α = ?, szukana wartość w zadaniu
β = 60o
Podstawa ostrosłupa to sześć przystających trójkątów równobocznych.
Popatrz na ΔACB, ΔCDE, ΔAED wiedząc, że
ΔACB równoboczny
E środek AB
DE wysokość ściany bocznej
sin α = ?, szukana wartość w zadaniu


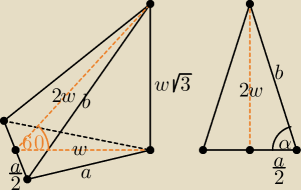 Włączam swój wpis, aby skorygować błędy w zapisach mojego imiennika (np. a2*a2 = a3)
Włączam swój wpis, aby skorygować błędy w zapisach mojego imiennika (np. a2*a2 = a3)