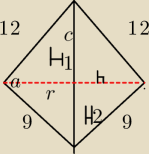
 Trójkąt o bokach długości równej 9 i 12 oraz kącie między tymi bokami o mierze 120 obraca się
dookoła najdłuższego boku. Oblicz pole przekroju osiowego i objętość powstałej bryły.
c=H1+H2
cos120=cos(180−60)=−cos60
Trójkąt o bokach długości równej 9 i 12 oraz kącie między tymi bokami o mierze 120 obraca się
dookoła najdłuższego boku. Oblicz pole przekroju osiowego i objętość powstałej bryły.
c=H1+H2
cos120=cos(180−60)=−cos60
| 1 | ||
c2=144+81−216*(− | ) | |
| 2 |
| 1 | ||
P= | *12*9*sin120 sin120=sin(180−60)=sin60 | |
| 2 |
| √3 | ||
P=54* | =27√3 | |
| 2 |
| 1 | ||
P= | ch | |
| 2 |
| 1 | ||
27√3= | *3√37*h | |
| 2 |
| 8√111 | ||
h= | ||
| 37 |
| 1 | 1 | 1 | 1 | |||||
V= | πr2*H1+ | πr2*H2= | πr2(H1+H1)= | πr2c= | ||||
| 3 | 3 | 3 | 3 |
| 1 | 7104 | 7104√37 | ||||
= | π* | *3√37= | ||||
| 3 | 1369 | 1369 |

 ?
?

