Równanie kwadratowe z wartością bezwzględną i parametrem heliksal: Proszę pomoc: x² − 6│x│ + 8 = m. Próbowałam metodą graficzną, tak jest dla mnie wygodniej i łatwiej. Mimo to ostateczne wyniki są niepoprawne

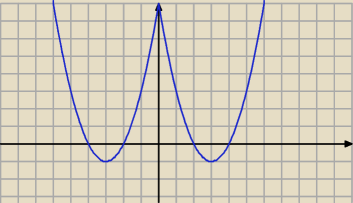
Saizou : −dla x<0 mamy x²+6x+8=m x²+6x+9−1=m (x+3)²−1=m −dla x≥0 x²−6x+8=m x²−6x+9−1=m (x−3)²−1=m a teraz....

heliksal: ok, wykres potrafię narysować. Jak wyznaczyć liczbę rozwiązań równania w zalezności od parametru m?

zombi: Siekasz twój wykres poziomymi liniami i sprawdzasz ile razy przeciąłeś wykres. Weźmy np. m=1 przecinam prostą poziomą na wysokości jeden i wykres Saizou przeciąłem 4 razy albo weźmy m=−3, przecinam prosta poziomą na wysokości −3 i nie przeciąłem wykresu ani razu, zatem dla m=−3, nie ma rozwiązań. Twoim zadaniem jest upakowanie wszystkich przypadków w ładne przedziały tzn. 2 rozwiązania, gdy m∊(.... ) itd.