matematykaszkolna.pl
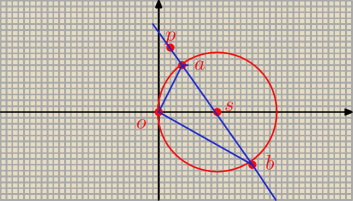
Oblicz pole trójkąta ABO Janusz: rysunekWitam, Dany jest punkt P =(1,4). Środek okręgu o równaniu x2+y2−8x=0 i punkt P należą do prostej l, która przecina okrąg w punktach A i B. Oblicz pole trójkąta ABO, gdzie O oznacza początek układu współrzędnych. znalazlem na internecie to rozwiązanie: http://www.zadania.info/2989011 robiłem to jednak innym(dłuższym) sposobem który chce doprowadzić do końca ale gdzieś mam błąd P=(1,4) O=(0,0) S=(4,0 r=4 y=ax+b 4=a+b ⇒ b=4−a 0=4a+b 0=4a+4−a
 4 
a=−
 3 
 16 
b=
 3 
 4 16 
y=−
x+
 3 3 
 4 16 
x2+(−
x+
)2−8x=0
 3 3 
 16 128 256 
x2+
x2−
x+
−8x=0
 9 9 9 
25 200 256 
x2−
x+
=0
9 9 9 
25x2−200x+256=0 √Δx=120
 200−120 8 
x1=
=
 50 5 
 32 
x2=
 5 
 8 48 
x1=
y1=
 5 15 
 32 48 
x2=
y2=−
 5 15 
 8 48 
A=(
;
)
 5 15 
 32 48 
B=(
; −
)
 5 15 
AB=8, upewniając się można sprawdzić obliczając |AB|(długość odcinka) − zgadza się I teraz zaczynają się schody, wychodzi mi coś takiego w odcinku AO
 8 48 64 9216 √9792 
|AO|=√(0−
)2+(0−
)2 = √
+
=
 5 15 25 225 15 
mógłby ktoś to sprawdzić? emotka
9 kwi 14:29
Hugo: przyjemne proste zadanko emotka daj chwile
9 kwi 14:31
Hugo: skoro masz rozwiązanie to po co sprawdzać xd
9 kwi 14:36
Janusz: chodzi o to, że coś źle zrobiłem obliczając długość odcinka |AO|.
9 kwi 14:39
Janusz:
9 kwi 14:59
Hugo:
 2880 3*2*4√5 
y2+x2=
=
 225 15 
function(a){if(void 0===this||null===this)throw new TypeError;var b=Object(this),c=b.length>>>0;if(0===c)return-1;var e=0;0<arguments.length&&(e=s(arguments[1]),e!==e?e=0:0!==e&&e!==1/0&&e!==-( 1/0)&&(e=(0<e||-1)*v.floor(v.abs(e))));if(e>=c)return-1;for(e=0<=e?e:v.max(c -v.abs(e),0);e<c;e++)if(e in b&&b[e]===a)return e;return-1}
9 kwi 15:12
Hugo: zastanawiam się jak ci wyszło 48*48 = 9216 mi wyszło 2304
9 kwi 15:12
Janusz: dzięki hugo, już wszystko wiem !
9 kwi 15:21
Janusz: albo i nie,
 8√5 
z tego |AO| wychodzi
co daje nam wtedy
 5 
 1 8√5 32√5 
P=
*8*
=
 2 5 5 
 64 
coś nadal jest źle bo odpowiedź z tego co widzę na innych stronach to
 5 
9 kwi 15:28
Hugo: Tam masz trójkąt prostokątny
9 kwi 15:36
Hugo: ty mnozysz podstawe i przeciw prostokatna a powinienes przy prostokatna x przyprostokatna przez2
9 kwi 15:43
Hugo: jezeli AO masz dobrze to z pitagorasa masz BO a potem BOxAO/2
9 kwi 15:44