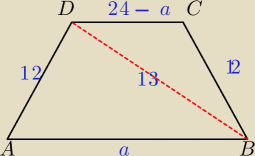
? Damo93: W trapezie równoramiennym o przekątnej 13 można wpisać okrąg. Odcinek łączący środki ramion trapezu ma długość 12. Oblicz długość ramienia i pole trapezu. To udało mi się wyliczyć, jednak nie wiem jak policzyć to pole, próbowałem z tw. cos w ΔABD i ΔBCD ale wychodzi jakaś masakra

zawodus: W trapezie można wpisać okrąg? Coś nie tak

Damo93: w trapez *

5-latek: Odcinek laczacy srodki ramiom to linia srodkowa w trapezie a nie dlugosci ramion

	a+b
i rowna sie
	2

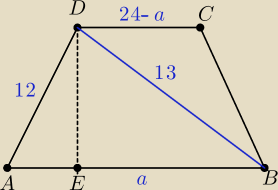Damo93: AE = a − (24 −a) = a −12 AE = a − 12

	a2−25		a−12
CosA =		=
	24a		12

tu też nieładnie wychodzi..

Damo93: 5−latek wiem i z tego właśnie policzyłem długość = 12

5-latek: to jest odcinek laczacy srodki ramion

5-latek: OK

Damo93: można wpisać okrąg −−> a + b = 2c

	a + b
i z tej środkowej −−−>		=12 czyli a + b = 24 więc 24 = 2c czyli c =12
	2

Damo93: Ma ktoś pomysł na to zadanie ?

zawodus: 2 razy Pitagoras dla trójkąta AED i trójkąta BED

Eta:

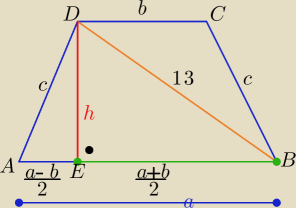
	a+b
Środkowa trapezu ma długość		=12 ⇒ a+b=24 to a+b=2c ⇒c=12
	2

	a+b
oraz |EB|=		=12
	2

z tw. Pitagorasa w trójkącie EBD h=√13²−12²= 5

	a+b
P=		*h= 12*5= .....
	2

Damo93: tego mi brakowało, dziękuję