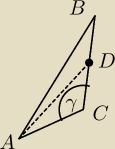
 Wyznacz cosγ z Tw Cosinusów anastępnie z tego tw IADI
Wyznacz cosγ z Tw Cosinusów anastępnie z tego tw IADI
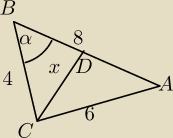 Liczysz wartość cos(α) dla dużego trójkąta: 62=42+82−2*4*8*cos(α). Piszesz twierdzenie
cosinusów dla trójkąta BCD: x2=42+(82)2−2*4*82*cos(α), podstawiając cos(α)
wyliczone z dużego trójkąta.
Liczysz wartość cos(α) dla dużego trójkąta: 62=42+82−2*4*8*cos(α). Piszesz twierdzenie
cosinusów dla trójkąta BCD: x2=42+(82)2−2*4*82*cos(α), podstawiając cos(α)
wyliczone z dużego trójkąta.
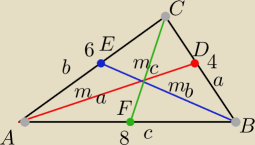 |AB|=c=8
|BC|=a=4
|AC|=b=6
|AB|=c=8
|BC|=a=4
|AC|=b=6
| 1 | ||
ma= | √2(b2+c2)−a2 | |
| 2 |
| 1 | ||
ma= | √2(36+64−16} | |
| 2 |
| 1 | 1 | |||
ma= | *√184= | *2√46=√46 | ||
| 2 | 2 |
| 1 | ||
mb= | *√2(a2+c2)−b2 | |
| 2 |
| 1 | ||
mb= | p[124} | |
| 2 |
| 1 | ||
mc= | √2(a2+b2)−c2 | |
| 2 |
| 1 | ||
mc= | √2(16+36−64} | |
| 2 |
| 1 | ||
mc= | √40 | |
| 2 |
| 1 | ||
mc= | *2√10=√10 | |
| 2 |
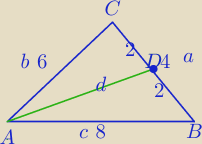
| a | ||
Wzór: b2+c2=2*d2+2*( | )2 | |
| 2 |
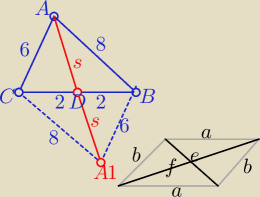 w każdym równoległoboku o bokach dł. a i b i przekątnych dł .f i e
zachodzi równość
f2+e2=2a2+2b2
zatem
(2s)2+42=262+282 ⇒ s2=46
s= √46
w każdym równoległoboku o bokach dł. a i b i przekątnych dł .f i e
zachodzi równość
f2+e2=2a2+2b2
zatem
(2s)2+42=262+282 ⇒ s2=46
s= √46