? Damo93: Oczywista oczywistość

	1		1		1		7
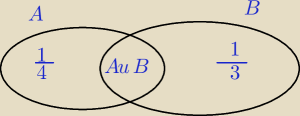
Zad. Wykaż, że jeżeli A, B ∊ Ω oraz P(A) =		i P(B)=		to		≤P(A u B)≤
	4		3		3		12

Mam problem z tym typem zadań. Nie wiem jak to wyjaśnić bo to jest przecież oczywiste.. nie wiem czy tu muszę jakoś konkretnie na wzorach pokazać czy można to jakoś słownie wykazać?

	1		1
np. że P(A u B) ≥		− to jest przecież oczywiste, ponieważ P(B) =		więc suma musi
	3		3

być większa ewentualnie równa gdy P(A) ∊ P(B) koniec dowodu ! nie wiem co mam tu więcej pokazać.

	7
dalej P(A u B) ≤		− to samo co wyżej skoro A = 1/4 B= 1/3 to suma max. może być 7/12
	12

przy założeniu że są to zbiory rozłączne w przeciwnym razie jest < 7/12... tu skorzystał z wzoru z tablic: P(A u B) ≤ P(A) + P(B) Nie wiem czy to wystarczy, nie ogarniam tych zadań..

Piotr 10: P(A∪B)=P(A)+P(B) − P(A∩B) 0 ≤ P(A)+P(B) − P(A∩B) ≤ 1 0 ≤ P(A)+P(B) − P(A∩B) (największe to będzie, gdy P(A∩B)=0 ) P(A)+P(B) ≥ 0 Inaczej mówiąc P(A∪B)_max ≤ P(A)+P(B)

1		1
	+		≥ 0
4		3

	7
P(A∪B)max ≤
	12

	1
P(A∪B)min gdy P(A∩B)=		wtedy cały zbiór A zawiera się w zbiorze B
	4

	1
czyli mamy P(A∪B)min ≥ P(A)+P(B) − P(A∩B) ≥
	3

Damo93: właściwe to jest to samo co napisałem tylko że trochę inaczej pokazane,

PW: Rozumujesz prawidłowo, choć sposób zapisania tego rozumowania zachwycający nie jest.