prosze o pomoc Jx: W trójkąt prostokątny wpisano okrąg o promieniu r. Na tym samym trójkącie opisano okrąg o promieniu R. Oblicz pole tego trójkąta.

norka:

marysia: P=2Rr+r²

Eta: Jx już zapewne zdał maturę

pigor: ..., krecik zmienił się w ... norkę: no to z warunków zadania i własności Δ prostokątnego: c=2R i 2r=a+b−2R ⇒ a+b=2(r+R) /² ⇔ a²+b²+2ab= 4(r+R)² ⇔ ⇔ 2ab= 4(r+R)²−c² ⇒ 2ab= 4r²+8rR+4R²−4R² /:4 ⇔ ⇔ ¹₂ab= r²+2rR ⇒ S=r(r+2R) − szukane pole trójkąta.

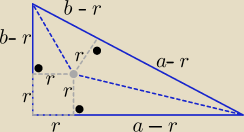Eta: 2 sposób c=2R , 2r=a+b−c ⇒ a+b=2R+2r

	a+b+c
P=p*r , p=		= 2R+r
	2

P=(2R+r)*r 3 sposób a−r+b−r=c =2R

	(b−r)*r		(a−r)*r
P=r2+2*		+2*		= r2 +(a−r+b−r)*r= r2+2R*r=r(2R+r)
	2		2