Pilne zadanie z planimetrii.:) Blue:

	|AP|
W trójkącie ABC dwusieczna kąta ACB przecina bok AB w punkcie P. Wykaż, że		=
	|AC|

	|BP|
		. Ja wpadłam tylko na takie coś, że ten podzielony kąt ma 2γ, czyli jak go
	|BC|

podzielimy to powstaną dwa trójkąty o kątach ostrych γ, α i γ, β. I zapisałam taki wniosek , że sinα = cosγ oraz sinβ= cosγ , a więc sinβ = sinα. Czy to wystarczy? Czy już coś udowodniłam, wykazałam, bo mi się wydaje, że nie do końca ... Pomożecie Proszę Was

Blue: Błagam o pomoc :C

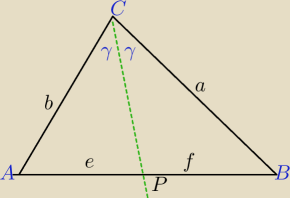Mila: Niestety , trzeba inaczej. To jest twierdzenie o dwusiecznej kąta wewnętrznego w trójkącie. Jest wiele dowodów tego twierdzenia. Oto jeden z nich , dość prosty. Stosunek pól trójkątów o równej wysokości równy jest stosunkowi długości ich podstaw⇔

	e
U{PAPC}{PCPB=		, gdzie AP=e, BP=f
	f

	1
PΔAPC=		*b*|PC|*sinγ
	2

	1
PΔCPB=		*a*|PC|*sinγ
	2

1   *b*|PC|*sinγ 2		b
	=		⇔
1   *a*|PC|*sinγ 2		a

b		e		e		f
	=		⇔		=		⇔
a		f		b		a

|AP|		|BP|
	=
|AC|		|BC|

Blue: Nie ma jakiegoś prostszego sposobu? Czy ten jest najprostszy?

Mila: Według mnie to najprostszy sposób, przecież pole Δ umiesz obliczyc. Czego tu nie rozumiesz? Narysuj wysokość Δ, jest wspólna dla obu wymienionych Δ.

	1
PΔAPC=		e*h
	2

	1
PΔCPB=		f*h
	2

PΔAPC		e
	=
PΔCPB		f

Możesz skorzystac z tw. sinusów. Jest więcej rachunków.

Mila: Nawiasem mówiąc, w Gm taki dowód z polem się podaje.

Blue: Ej, w zasadzie to to twierdzenie jest bardzo logiczne Chyba rzeczywiście prostszego sposobu nie ma/

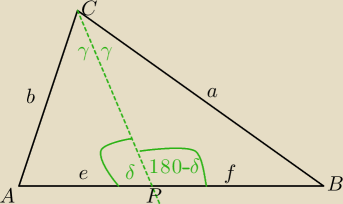Mila: II sposób Z tw. sinusow. W ΔAPC:

	e		b
(1)		=
	sinγ		sinδ

W ΔCPB:

f		a
	=		⇔
sinγ		sin(180−δ)

	f		a
(2)		=
	sinγ		sinδ

Dzielę stronami (1) przez (2)⇒

e		b
	=		⇔
f		a

e		f
	=
b		a

cnw

pigor: ...no to może np. tak : przez punkt B poprowadź prostą równoległą do CP, aż przetnie się z przedłużeniem AC w punkcie R, wtedy łatwo wykazać, że |CR|=|BC|=a (dlaczego ?), a stąd i tw. Talesa

e		f		e		f		|AR|		|BP|
	=		⇔		=		⇔		=		c.n.w. . ...
b		|CR|		b		|a		|AC|		|BC|

Mila: Witaj , pigor, dla każdego coś miłego.