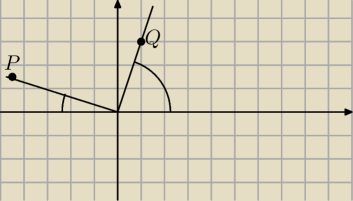
sinus marcela: Punkt P należy do ramienia końcowego kąta alfa, a punkt Q − do ramienia końcowego kąta beta. Oblicz sin alfa − sin beta P(−9,3) Q(2,6)

marcela: CHYBAba sobie PORADZIŁAM.... TERAZ MAM PROBLEM PRZY TAKIM SAMYM POLECENIU.... TYLKO NALEZY OBLICZYC SIN ALFA + SIN BETA P(−2, √2 Q√2przez 2 ,1) policzyłam r= pierwiastek z 6 sin alfa wyszedł mi pierwiastek z 2 przez pierwiastek 6 czyli po usunieciu niewymiernosci pierwiastek z 3 przez 3

marcela: to było P

marcela: a Q r=pierwiastek 3/2 sin beta 1 przez pierwiastek 3/2

marcela: i nie wiem jak dalej to policzyc....

zawodus: i definicja sinusa

zawodus: bardzo chaotycznie piszesz weź głęboki oddech i postaraj się poprawić zapis

marcela: złapałam natchnienie... muszę sie przyznac ze nie potrafie precyzyjnie poruszac sie na portalu...

marcela: polecenie jest następujące.. Punkt P należy do ramienia końcowego kąta alfa, a punkt Q − do ramienia końcowego kąta beta.

marcela: OBLICZ SIN ALFA + SIN BETA P(−2, √2) Q(√2przez 2 ,1)

marcela: policzyłam P r= √6 sin alfa wyszedł mi pierwiastek z 2 przez pierwiastek 6 czyli po usunieciu niewymiernosci pierwiastek z 3 przez 3

marcela: Q r=pierwiastek 3/2 sin beta 1 przez pierwiastek 3/2

marcela: i teraz mam problem z tym dodawaniem ...proszę o pomoc