aa Hugo: Suma trzech początkowych wyrazów rosnącego ciągu geometrycznego jest równa sumie odwrotności tych wyrazów. Oblicz te wyrazy jeżeli szósty wyraz ciągu jest równy 16. zatem

	1		1		1
a1+a1q+a1q2 =		+		+
	a1		a1q		a1q2

a₆=16=a₁q⁵

Hugo: zw 2 min //ale to jest chyba prostsze

J: OK.

Marcin: Wyznacz z pierwszego a₁ i będziesz mieć q Uważaj na to, że ma być rosnący

Hugo: Veni, vidi, vici a₁=16/q⁵

16		16		16		q5+q4+q3
	+		+		=
q5		q4		q3		16

16		16q		16q2		q5+q4+q3
	+		+		=
q5		q5		q5		16

16+16q+ 16q2		q5+q4+q3
	=
q5		16

	1+q+ q2		q3(q2+q+1)
16		=
	q5		16

1+q+ q2
	= q2+q+1
q2

1+q+ q² = q⁴+q³+q² 0 = q⁴+q³−1−q

Hugo: 0=q³(q+1)−(q+1) 0=(q³−1)(q+1) q₁= 1 v q₂ = −1 Ale z uwagi że Ciąg jest rosnący ! a na pewno monotoniczny q>0 q=1 ! (tak to jest silnia z jeden )

Hugo: a₁q⁵=16 a₁*1⁵=16 a₁ = 16 a₁=16 a₂=16 a₃=16 .... a₆9=16

Marcin: jeżeli q=1, to ciąg nie jest rosnący. Przelicz jeszcze raz

Hugo: q = 2 a₁ = 1/2

Hugo: http://zadane.pl/zadanie/3884938 .. aczkolwiek zaraz to i tak muszę przeanalizować ..

J:

	1
a6 =(		)5 = ..
	2

Marcin:

Hugo: // Wgl zaczął się nowy sezon gry o tron na HBO ! mam nadzieje że oglądacie

bezendu: Nie oglądam TV

Marcin: Już pooglądałem

Marcin: Ale polecam książkę

J: Wycofuję 20:27

Hugo: J:

	1
a6 = 1/25 =		w linku mam rozpisane sb analizuje co i jak.. smutne że wciąż mi
	32

nie wychodzi a matura za 28 dni

J:

	1
Nie .. to ja się pomyliłem... a6 =		*25 = 16
	2

Hugo: właśnie FOOCH na książke bo tam fabuła sięga dalej; hmm jedyna fajna książka jaką znałem to hobbit i wdł mnie film zrą*ali.. co do G.of T książka a serial.... taką np. Deneris w książce w HD nie zobaczysz 8)))

Hugo: J: Ile miałeś z matury jeżeli można spytać

J: Wtedy jeszce była inna skala ocen i zupełnie inna matura ... ale najwyższą

Marcin: Khaleesi w HD już dzisiaj widziałem

Hugo: Nauczcie mnie w miesiac matury; wiem że największa skuteczność jest uczenie się nie tyle pewnych braków podstaw ale już typowo pod zadania; pod mature.. rozwiązuje sb matury.. myślałem nad zakupem zbioru zadań miałem polecone z Kiełbasy (autor) .. u nas Pani używa nowej ery Marcin: I jak, wciąż ta sama soczyście *ejakuacyjnie* wyglądająca bohaterka jak w III cz. 8))? // Sam czekam aż małego króla ukatrupią

Marcin: Nie chce CI spojlerować co do Joffreya Czekaj Soczyście

Marcin: Ale teraz nie ma gry o tron, trzeba się uczyć

Hugo: przeliczyłem jeszcze raz tym razem poskracałem od razu i mi wyszło : )) 'Nie kraczmy działajmy' kolejne przykłady są do zrobienia liczę że potowarzyszycie jeszcze

Bogdan: Obliczenia są prostsze, jeśli oznaczymy pierwsze trzy wyrazy rosnącego ciągu geometrycznego

	a
(an): a1 =		, a2 = a, a3 = ag oraz mamy: q > 1, a6 = a2q4 = aq4 = 16.
	q

a		q		1		1
	+ a + ag =		+		+		/ *ag ⇒ a2(1 + q + q2) = g2 + q + 1
q		a		a		aq

stąd a² = 1 ⇒ a = 1 lub a = −1 czyli a₂ = 1 lub a₂ = −1 a₆ = aq⁴ ⇒ 16 = 1*q⁴ ⇒ q = 2 lub q = −2 (sprzeczność) lub 16 = −1*q⁴ (sprzeczność)

	1
a1 =		, a2 = 1, a3 = 2
	2

Hugo: Oblicz iloraz rosnącego ciągu geometrycznego (a_n) jeżeli: a) a₄ = a₃+8 a₁+a₂+a₃=14 coś za proste

Marcin: aq³=aq²+8 a+aq+aq²=16 No i q=.. Próbuj najpierw sam

Hugo: Bogan: Im więcej zmiennych im więcej złożoności tym większa szansa na bład który może zepsuć całe zadanie, inaczej ukazujesz to zadanie : > przemyślałem i dość mi się to podoba dziękuję za mądrości //co do tego kolejnego zadania: szukamy q a₁q³=a₁q² + 8 => a₁(q³− q²) = 8

	14
a1 + a1q + a1q2=14 /:a1 => a1(1+q+q2)=14 => a1 =
	1+q+q2

...: ... utwierdzam się w przekonaniu, że Hugo to drugie wcielenie kamczatki − JEŚLI NIE NUCZYSZ SIĘ PODSTAW ... próżny Twój "trud" ... To, że inni rozwiążą Ci określoną ilość zadań nie daje Ci praktycznie NIC. TRACISZ CZAS. Tylko samodzielne rozwiązywanie (sporadycznie z pomocą) "pozostawia ślad". A sam nic nie zrobisz nie znając podstaw ! Ani teraz ani na maturze !

zawodus: ciekawsze czy to lepsze wcielenie?

Hugo: // do której będziesz tu siedział

14
	* (q3−q2)=8
1+q+q2

14³+14q²=8+8q+8q²

Marcin: Huugo no i jak już powyznaczałeś, to ile Ci wyszło?

Marcin: No i masz dobrze, ale Ci uciekło na początku q³ 14q³

Hugo: sprawdzalem twoja czujnosc 8)... 0= −7q³ −3q² +4q +4 ale proboje to podzielic ten wielomian i cos nie da sie

Marcin: 14q³−14q²=8+8q+8q² Jeszcze Ci się z minusa zrobił plus

Hugo: to by wiele wyjaśniało w(x)−14q³+22q²+8q+8=0 −7q³+11q²+4q+4=0 w(2)? ... ... w(2)=0 Horner ! w(x)= (−7x²−3x−2)(x−1) w tym pierwszym delta ujemna −> 9 − 56 <0 więc rozw to x = 1 v x = 2 gdzie x = q Ale że jest to rosnący to 1 nie może być I jedyne rozw to 2

Marcin: skąd Ci się to (x−1) wzięło? Wielomian dzielisz przecież przez (x−2)

Hugo: Hugo is also "Happy" ♪♪♪.... Co do porównania do kamczatki... + Ja robie te zadania sam a gdy nie wiem przełamuję dzięki wam bariery ucząc się. + Uważam że lepiej tu napisać niż pozostawać w martwym punkcie i się dołować XD + Macie tu również maturki z rozwiazaniami więc sb fajnie śledze + Jeżeli coś większego mi nie jest jasne w kwestii bardziej metodystycznej to znajduję pomoc Więc uważam że tak nie do końca się tu cofam XD jestem wdzięczny że takie forum istnieje. Chciałem się dostać na budownictwo... aczkolwiek chyba się nie dostane.

Hugo: racja .. nie wiem

Hugo: Podpunkt b) 1)a₃=3 2)a₁a₂a₃a₄=108 1)a₃=3 aq²=3 2)a⁴*q⁶=108 1)2)

81
	=108
q2

81=108q²

	√3
q=
	2

Marcin: Sposób rozwiązania jest identyczny, także nawet Cie nie sprawdzam

Hugo: Marcinie a ty jesteś studentem? jeżeli tak to który rok i jaki kierunek jak można spytać?

Marcin: Klasa maturalna, technikum Mooże przyszłoroczny student

Hugo: 7) Dany jest ciąg geometryczny (a₂) b) Wiedząc że suma dwudziestu początkowych wyrazów ciągu an jest równa 124 a suma dwudziestu początkowych wyrazów ciągu b_n jest równa 31 oblicz iloczyn dwudziestu początkowych wyrazów ciągu a_n. S_a20=124 S_b20=31

Hugo:

	1
i w pod pkt a) jest treść; Uzasadnij że ciąg bn=		także jest ciągiem geometrycznym
	an

I nie wiem czy stąd można zaczerpnąć zależność a_n i b_n ... teoretycznie inny podpunkt ale troche mało mi sie wydaje danych mamy

Marcin: Podziękuj Irenie http://screenshu.com/static/uploads/temporary/ts/t1/9u/mqr2wj.jpg

Hugo: S_a20=a₁(1+q+q²+q³+q⁴...q¹9)=124 S_b20=a₁(1+q+q²+q³+q⁴...q¹9)=31 szukamy: a²⁰*q¹⁹⁰

Hugo: Ireno dziękuję ci (już ogarniam )

Marcin:

Hugo: nie wiem co począć; plan ambitny zakłada maturke z zadań info co mieliśmy na kiedyś ale mamy omawiać i tak było by nonszalancko HUGO mądry na tle klasy 8) + mam na jutro lekturke INNY świat

Marcin: Wy się jeszcze w szkole uczycie? serio? Ja mam już od jakiegoś czasu pełny luzik

Hugo: ja liceum nie wiem xd do konca tygodnia wystawienie ocen http://www.zadania.info/95094 .. zw2min.. jakies ~2 zadanka o ile bedzie ci sie chcialo i lulh

Marcin: Mi się zawsze chce pomagać przy matmie, ale nie zawsze potrafię Tak się przyzwyczaiłem do codziennego robienia matmy, że aż się obawiam co to będzie po maturze

jakubs: Po maturce zawsze możesz się uczyć materiału na studia, ale ja bym polecał odpocząć

Marcin: Jak po maturce będę czuł że się gdzieś dostanę, to na pewno będę coś próbował ogarnąć

Hugo: Sądzę że też jak tu siedzicie i pomagacie to też się człowiek udoskonala : > No ale dobre pytanie co po maturce Z punktu A = (17 ,1 6) poprowadzono styczne do okręgu o równaniu 2 2 (x + 3) + (y − 1) = 1 25 . Oblicz długość odcinka łączącego punkty styczności.

bezendu: Zapisz porządnie to pomogę !

Hugo: wybacz zad 8 http://www.zadania.info/95094

bezendu: (x+3)²+(y−1)²=125 S=(−3,1) r=5√5 A=(17,16) y=ax+b 16=17a+b b=16−17a y=ax+16−17a −ax+y+17a−16=0 Dokończ wstawiając do wzoru na odległość punktu od prostej

Marcin: Ja bym sobie policzył odległość od środka tego okręgu do punktu A. Później mając promień liczyłbym długość Od punktu A, do punktu styczności dalej bym coś pewnie wykombinował

Hugo: troche to zawile dla mnie

	|Ax+By+C|
d=
	√A2+B2

mam wstawic pkt A oraz ta prosta w ost. linijce 17a −16+16−17a/√a²+1 ? prosze o wskazowki

bezendu:

|−ax+y+17a−16|
	=5√5
√a2+1

−3a+1+17a−16|
	=5√5
√a2+1

|14a−15|=√a²+1*5√5 /² 196a²−420a+225=125a²+125 Teraz kończ już sam Marcin jedno ?

Hugo: Marcin: odleglosc od S do A to √689

Hugo: juz paczam

Marcin: Się wkręciłeś w piwkowanie

bezendu: Namówiłeś mnie

Hugo: delta jest dziwna... 20√370

	105−5√370		105+5√370
a1=		v a2=
	49		49

bezendu: Nie wiem, zakładam, że umiesz dodawać.

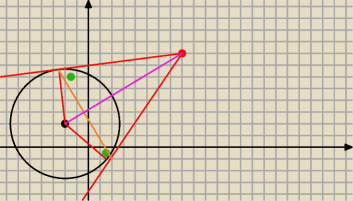
Marcin: Masz wyliczyć pomarańczową odległość. Widzisz coś?

Marcin: Hugoo zostaw naukę i chodź na piwko, tak jak ja i bezendu

Marcin: Źle masz policzoną odległość tak w ogóle. S=(−3;1) A=(17,16) Jak to liczysz?

Hugo: wole Deneris ! .. Okej czyli obliczylem ' a' ktore tyczy sie prostej ax+b=y ... potrzebuje te dwa pkt na okregu by wyznaczyc odleglosc miedzy nimi wiec do prostej podstawiam okrag i mi wyjda dwa pkt? dobrze mysle?.. jak nie to jutro sobie na spokojnie siade

Hugo: |AS|=25

Marcin: Masz równanie prostych, które są styczne, o to Ci chodzi? Jeżeli to masz, to faktycznie możesz policzyć te dwa punkty, a później odległość między nimi.

Marcin: Teraz dobrze

Hugo: dobra nie mam sil jutro popaczam .. musze sam zrobic bo sie nie naucze.. dziekuje bardzO zA pomoc ! kazdemu!≈

Marcin: Dokładnie. Musisz sam zrobić bo się nie nauczysz Siemano