uzasadnij, ze bartiw95: 1. Uzasadnij ze suma dlugosci przekatnych w trapezie jest wieksza od sumy dlugpsci bokow rownoleglych. 2. Wiedzac ze p(a)=1/2 , p(b)=2/3 , wykaz ze p(a U b) >1/6

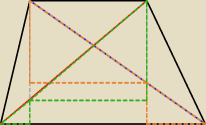
wredulus_pospolitus: 1) wskazówka: 2) no i w czym problem P(AuB) ≥ P(A) + P(B) − P(Ω)

pigor: ..., a nie miało tam być p(a ∩ b) >1/6 , a może nawet p(a ∩ b) ≥ 1/6

pigor: ..., 1) niech a || b − długości podstaw trapezu i punkt przecięcia przekątnych e,f dzieli je na odcinki tak, że x+y= e i z+t= f , to z nierówności Δ : x+t >a i y+z >b /+ stronami ⇒ x+y + t+z >a+b ⇔ e+f > a+b c.n.uzas. . ...

pigor: ..., cofam pytanie do zadania 2, a więc 2) Wiedząc, że P(A)=¹₂, P(B)=²₃ wykaż, że P(AUB) > ¹₆ −−−−−−−−−−−−−−−−−−−−−−−−−−−− widzę to np. tak : A⊂ AUB i B⊂ AUB ⇒ P(A)≤ P(AUB) i P(B)≤ P(AUB) /+ stronami ⇒ ⇒ P(A)+P(B) ≤ 2P(AUB) ⇔ P(AUB) ≥ ¹₂(P(A)+P(B)) ⇔ ⇔ P(AUB) ≥ ¹₂ (¹₂+²₃)= ¹₂ (³₆+⁴₆)= = ¹₂*⁷₆= ⁷₁₂ > ⁶₁₂= ¹₂ c.n.w. ...

pigor: ...o kurcze ale jaja, przepraszam, to nie to miałem wykazać oj znikam z forum, aby nie majaczyć