trygonometria Robaczek: https://matematykaszkolna.pl/strona/1581.html Jak tam doszli do tego wzoru.. bo nie rozumiem?

ZKS: Napisz trochę jaśniej o co chodzi.

Piotr: jakiego wzoru ?

maturka: a co ile okresów sinus przyjmuje wartość 0? co kπ podstaw za k jakąś liczbę całkowita

Robaczek: x=kPI, wybaczcie, ale nie wiem jak się za to zabrać. Wiem w jakich miejscach przecina oś, jednakże nie rozumiem odpowiedzi "kPI".

Robaczek: Maturka: dziękuje, nie wpadłbym na to pomimo, że odpowiedź jest tak prosta.

maturka:

Robaczek: Zadziwiająco dużo osób tutaj o tej porze dzisiaj

Robaczek: Eh jednak za nic w świecie nie mogę zrozumieć tego co tutaj się dzieje i jak do tego dojść. Rozwiąż równanie: sinx=0 cosx=−1 Mógłby ktoś łopatologicznie wytłumaczyć jak do tego dojść?

Piotr: hmm, co tu tlumaczyc. patrzysz dla jakich argumentow (x) funkcja przyjmuje dana wartosc. i tyle.

Robaczek: Nie, bo dla sin=0 kPI, ale patrząc na cosinusa to również w tych samych punktach przyjmuje te wartości ...,−2pi,−pi,pi,2pi,4pi... wiec też by pasowało kx

Robaczek: dobra widzę.

Robaczek: Mój problem polega na tym, że widzę, gdzie się przecinają, ale nie umiem robić z tego wzoru. Gdyby ktoś był tak miły.

Piotr: jakiego wzoru ? tu nie ma wzoru. patrzysz gdzie przecina i jaki okres ma funkcja. nic wiecej.

maturka: sinα=a a∊<−1,1> α=x+2kπ α=π−x+2kπ

maturka: np. sin= ∫3/2 x= π/3 to x1=π/3+2kπ x2=π−π/3+2kπ =2π/3+2kπ

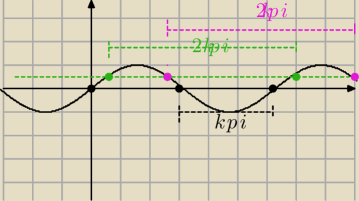
asdasd: k∊C sinx=0 x=0+kπ −−−−−−−−−−−−−−−−−−−−−−−−−−−−− k∊C

	1
sinx=
	2

	π
x1=		+2kπ
	6

	5π
x2=		+2kπ
	6