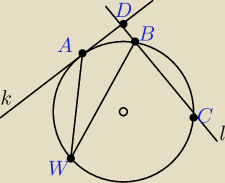
plani jerey: prosta k jest styczna do okręgu w punkcie A. Prosta l prostopadła do prostej k przecina okrąg w punktach B i C zas prosta k w punkcie D tak, ze |BC|=4,8|AD|. Oblicz tangens kąta ostrego AWB wpisanego w dany okrąg. zastosowałem twierdzenie o odcinkach siecznej i stycznej: AD²=DB*BC AD²=DB*4,8AD

	AD
DB=
	4,8

z twierdzenia pitagorasa licze AB

	√24,04AD
AB=
	4,8

i nie wiem co dalej. moze jakies wskazówki?, w ogole w dobrym kierunku zmierzam?

Godzio: Poprowadź odcinek AC, czemu jest równy kąt ACD

jerey: ∡ACD=∡AWB bo oparty na łuku AB

Godzio: Skup się na obliczeniu tangensa ACD i po zawodach

jerey: spróbuję cos zdziałać , jak cos będe pisał w temacie. dzieki za wskazówke ,

jerey: liczę juz któryś raz z kolei i wychodzi mi załosny wynik.

	24,04AD
obliczyłem DC=
	4,8

niech DC ⇒b AD⇒a

	a		4,8
tg=		⇒		=0,1996...
	b		24,04

pigor: ..., no to może np. tak : niech |∡AWB|=γ − ostry i tgγ=? oraz |AD|=b, |DB|=a, dla uproszczenia zapisu, to z 3−ech tw.: 1) o kącie wpisanym opartym na tym samym łuku ; 2) tw. o kącie stycznej i siecznej; 3) tw. odcinkach stycznej i siecznej z punktu poza okręgiem i warunków zadania, masz np. takie równanie : b²=a(a+4,8b) ⇔ b²=a²+4,8ab /:b² ⇔ 1= (^a_b)²+ 4,8^a_b ⇔ ⇔ 1= tg²γ+4,8tgγ /+ 2,4² ⇔ tg²γ+2*2,4tgγ+ 2,4²= 1+2,4² ⇔ ⇔ (tgγ+2,4)²= 6,76 ⇒ tgγ+2,4=2,6 ⇔ tgγ= 0,2 . ...

Godzio: Taki jest chyba wzór: |AD|² = |DB| * |DC|

jerey: a skąd to b²=a(a+4,8b) tego nie rozumiem

jerey: aaa juz wiem. Godzio ja zle wzór zapisałem. i wszystko nie tak przez ten wzór

jerey: w kazdym razie pigor dzieki , juz wiem skąd to sie bierze

pigor: ... tak prawdę mówiąc, spojrzałem na to z ... góry i widzę, że tw.2) w tym moim rozwiązaniu do niczego nie było mi potrzebne

student: Godzio czy mógłbyś looknąć na mój post? Bardzo Cię proszę,chociaż tak powierzchownie,i wyraził swoje zdanie na ten temat

pigor: ..., tak miałeś ... nieco zły ten właśnie wzór .