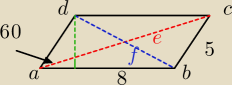
Oblicz długości przekątnych równoległoboku Janusz: W równoległoboku ABCD długość boku AB wynosi 8, długość boku BC jest równa 5, a miara kąta ostrego ma wartość 60. Oblicz długości przekątnych danego równoległoboku. Korzystam z twierdzenia cosinusow.

	1
f2=25+64−80*
	2

f²=89−40 f>0, f=7 i teraz mam problem, jak mogę wyliczyć długą przekątną? podajcie mi sposoby, te najłatwiejsze oczywiście widziałem na internecie wzór na zależność w równoległoboku: e²+f²=2(a²+b²), może wyliczę tym sposobem ale wychodzi dość kiepski wynik. Obliczyłem też wysokość:

	h
sin60=
	5

	5√3
h=
	2

ale ona na wiele się tutaj już chyba nie zda Jakieś propozycje?

marta: e=7 , f=√129

Bogdan: cos(180^o − α) = −cosα

	1		1
Np.: cos60o =		, cos120o = −
	2		2

Janusz: dobra, wszystko jasne dzięki

Bogdan:

	1
e2 = 64 + 25 + 80*		= ...
	2